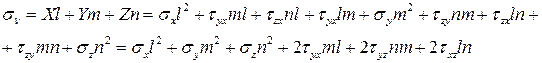Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение напряжений на произвольной площадке
|
|
Выделим внутри рассматриваемого элементарного куба произвольную секущую площадку А:
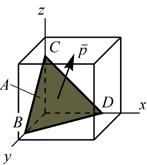
Получим элементарный тетраэдр, на наклонной площадке BCD которого возникает вектор полного напряжения  .
.
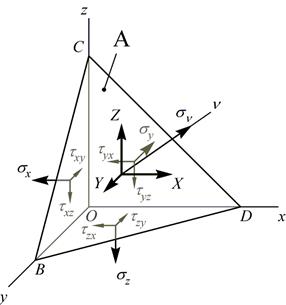
Пусть даны шесть компонент напряжений: 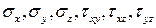 , действующих в координатных гранях тетраэдра. Определим X, Y, Z – проекции вектора полного напряжения
, действующих в координатных гранях тетраэдра. Определим X, Y, Z – проекции вектора полного напряжения 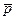 , действующего на площадке BCD.
, действующего на площадке BCD.
Введем следующие обозначения:
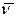 - нормаль к площадке BCD,
- нормаль к площадке BCD,
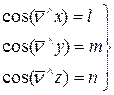 - направляющие косинусы, которые определяют положение площадки BCD.
- направляющие косинусы, которые определяют положение площадки BCD.
Обозначим площадь рассматриваемой площадки ABCD=A, тогда площади остальных граней: ABCO=A× l; AOCD=A× m; ABOD=A× n.
Запишем условия статического равновесия для системы сил, действующей на грани выделенного тетраэдра:
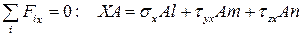 ,
,
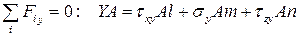 ,
,
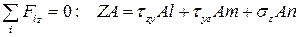 .
.
Откуда проекции вектора полного напряжения:
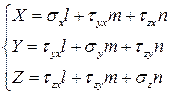
Таким образом, напряженное состояние в точке можно считать заданным, если известны напряжения на трех взаимно перпендикулярных площадках.
Нормальное напряжение на площадке BCD можно определить как сумму проекций компонент вектора полного напряжения Х, Y, Z на нормаль 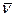 :
: