Решение плоской задачи О.К. Мора

Прямая задача Мора

Прямая задача Мора – это задача определения напряжений на произвольной площадке по известным главным напряжениям.

Рассмотрим элементарный объем, находящийся в условиях объемного напряженного состояния, причем грани этого объема являются главными площадками. Секущей площадкой, параллельной главному напряжению σ ₂, выделим из этого объема треугольную призму:

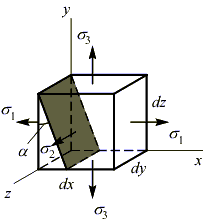
Для определения напряжений на произвольной секущей площадке, рассмотрим переднюю грань призмы

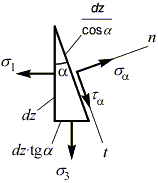
Запишем уравнения равновесия для системы сил, действующей на грани призмы.

Для оси, касательной к наклонной площадке :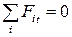

.

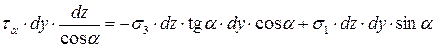Сокращая общие множители и умножая все слагаемые на 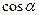, получим

,

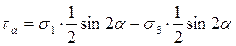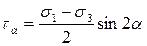. (2.2)

Для оси, нормальной к наклонной площадке :

,

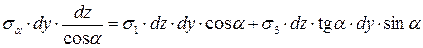откуда

.

Проведем следующие преобразования:

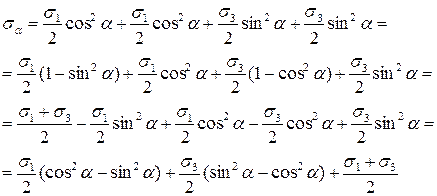
и получим:

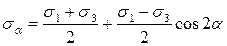. (2.3)

Возведем в квадрат каждую часть полученных выражений (2.2) и (2.3):

,

.

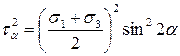Суммируя попарно левые и правые части, получим:

.

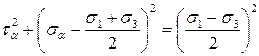Это уравнение в координатах t-s является уравнением окружности с центром в точке 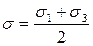, и радиусом :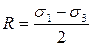

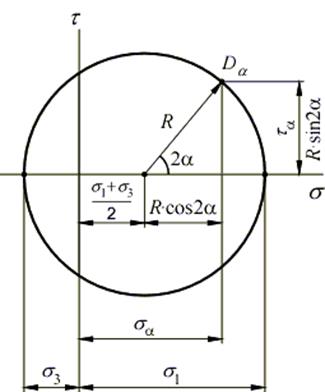
Полученная окружность называется кругом напряжений или кругом Мора. Круг Мора пересекает ось абсцисс в точках с координатами s ₁ и s ₃.

Определим координаты точки D_a:

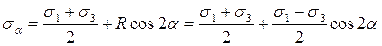, (2.4)

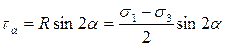, (2.5)

что совпадает с полученными ранее формулами (2.2) и (2.3).

Таким образом, каждой площадке, наклоненной под углом a к главным площадкам, на круге Мора соответствует определенная точка. Радиус этой точки составляет с осью абсцисс угол 2 a, а ее координаты определяют напряжения на площадке s_a и t_a.