Вынужденные колебания упругой системы с одной степенью свободы

Добавим к числу сил, действующих на систему, вынуждающую силу F ₀sinW t, где W - частота вынуждающей силы:

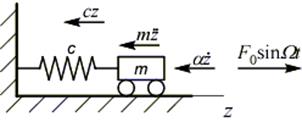
При этом уравнение равновесия принимает вид

.

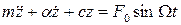Введем обозначение .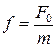

Таким образом, дифференциальное уравнение, описывающее вынужденные колебания упругой системы с одной степенью свободы с учетом сил сопротивления имеет вид:

.

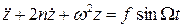Примем частное решение данного дифференциального уравнения в виде . Его первая и вторая производная имеют вид

,

.

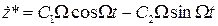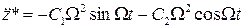Подставляя выражения для 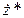и 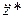в дифференциальное уравнение, получим

.

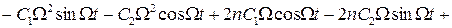
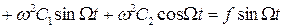
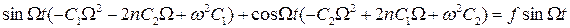Данное равенство будет выполняться, если

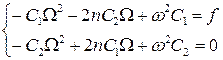
Из последнего уравнения выразим С₂:

,

.

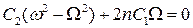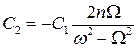Преобразуем первое уравнение:

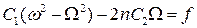
и подставим в него выражение для C ₂:

,

.

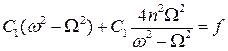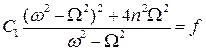Таким образом, коэффициенты уравнения колебательного процесса принимают вид:

; .

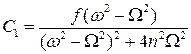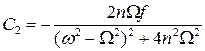Введем обозначения:

,

.

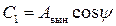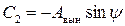С учетом этих обозначений уравнение вынужденных колебаний можно записать в виде:

.

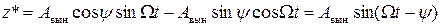Отсюда видно, что A _вын – амплитуда вынужденных колебаний, y – фазовый сдвиг между вынуждающей силой и вызываемыми ею колебаниями.

Определим амплитуду вынужденных колебаний:

,

,

.

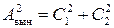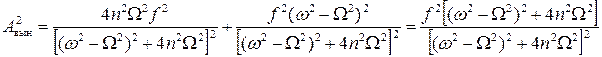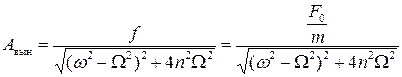Выразим массу из формулы для частоты собственных колебаний:

→ .

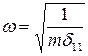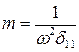Тогда амплитуда вынужденных колебаний вычисляется по следующей формуле:

.

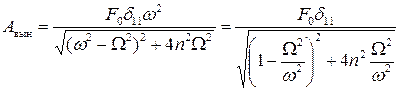Здесь 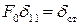– статическое перемещение точки, за колебанием которой мы наблюдаем. То есть, если амплитудную величину возмущающей силы приложить к данной точке статически (в направлении колебательного процесса), то эта точка получит статическое перемещение .

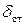Тогда представим формулу для амплитуды вынужденных колебаний в следующем виде:

,

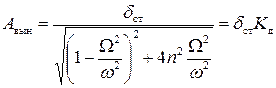где 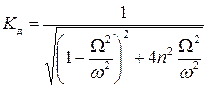- коэффициент динамичности.

Таким образом, амплитуда вынужденных колебаний (динамическое перемещение):

.

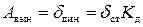В соответствии с законом Гука напряжение прямо пропорционально деформации, то есть

.

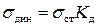Если 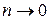либо 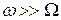, то коэффициент динамичности

.

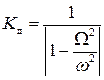График зависимости коэффициента динамичности от отношения частот вынужденных и собственных колебаний:

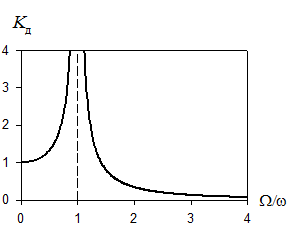
При 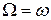: 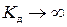– это случай резонанса.

Фазовый сдвиг:

.

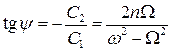При 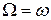фазовый сдвиг 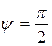, т.е. вынуждающая сила достигает максимального значения в момент, когда колебательная система проходит через состояние равновесия. Это и является причиной резонанса.

Удар

Ударом называется взаимодействие тел, при котором силы взаимодействия резко нарастают или ослабевают за короткий промежуток времени. Удар относится к динамическим видам нагружения.

Можно выделить три вида задач об ударе:

1. Задачи об изменении параметров движения взаимодействующих тел, решаемые аппаратом механики недеформируемого твердого тела.

2. Задачи о напряжениях и деформациях, возникающих во взаимодействующих телах, решаемые аппаратом механики деформируемого твердого тела.

3. Задачи об определении свойств материалов при ударе.

В курсе «Сопротивление материалов» решаются ударные задачи только второго вида: производится расчет на прочность и жесткость элементов конструкций при ударном нагружении. Более общий подход к решению таких задач был предложен доктором технических наук, основателем кафедры «Сопротивление материалов» Тольяттинского политехнического института Георгием Федоровичем Лепиным.