
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теория удара Лепина
|
|
Основные допущения:
1. Ударяющее тело абсолютно жесткое.
2. Материал ударяемого тела следует закону Гука.
3. Ударяемое тело имеет одну степень свободы.
4. Удар неупругий, т.е. ударяющее тело после удара не отскакивает, а движется совместно с ударяемым телом.
5. Кинетическая энергия ударяющего тела полностью переходит в потенциальную энергию деформации ударяемого тела, т.е. можно пренебречь контактными явлениями.
6. Деформация мгновенно распространяется по ударяемой системе, и все ее точки начинают движение одновременно, т.е. можно пренебречь волновыми явлениями.
Рассмотрим упругую систему в виде пружины длиной l и жесткостью c с грузом весом F 1. Пружина образует с горизонтом угол a и под действием веса груза имеет деформацию d. Абсолютно жесткое тело весом F движется со скоростью v под углом b к горизонту.

Определим перемещение упругой системы d д после удара (динамическое перемещение).
В соответствии с законом сохранения импульса, количество движения системы до и после удара одинаково. Проецируя количество движения на ось a, можно записать:
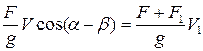 ,
,
где V 1 – скорость движения системы после соударения:
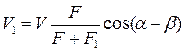 . (4.1)
. (4.1)
Воспользуемся теоремой о кинетической энергии:
T 2 – T 1 = I, (4.2)
где T 1, T 2 – кинетическая энергия в начале и конце ударного взаимодействия соответственно, I - работа всех сил на перемещении во время ударного взаимодействия.
Кинетическая энергия системы в начале взаимодействия равна
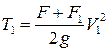 .
.
Подставляя сюда вместо V1 выражение (11.1), получим:
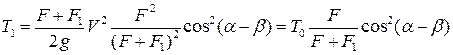 , (4.3)
, (4.3)
где 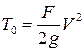 – кинетическая энергия ударяющего тела.
– кинетическая энергия ударяющего тела.
В конце ударного взаимодействия система неподвижна, и ее кинетическая энергия T2=0.
Работа внешних сил складывается из работы силы тяжести и силы упругости пружины:
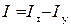 .
.
Работа силы тяжести системы на перемещении, вызванном ударом:
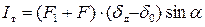 . (4.4)
. (4.4)
Рассмотрим зависимость силы упругости F у от перемещения d. По закону Гука 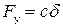 :
:
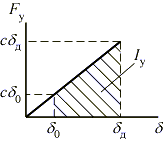
Как видно из графика, работа силы упругости на перемещении, вызванном ударом, определяется
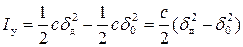 .
.
Представим жесткость пружины в виде  , где d 11 – податливость упругой системы (перемещение точки соударения под действием единичной силы, приложенной по направлению перемещения во время ударного взаимодействия). Тогда работа сил упругости
, где d 11 – податливость упругой системы (перемещение точки соударения под действием единичной силы, приложенной по направлению перемещения во время ударного взаимодействия). Тогда работа сил упругости
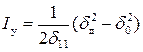 . (4.5)
. (4.5)
Формула (11.2) с учетом выражений (11.3), (11.4) и (11.5) принимает вид:
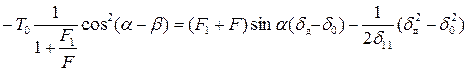 ,
,
откуда
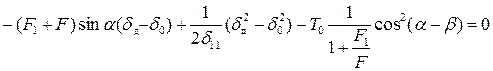 ,
,
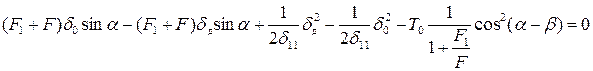 ,
,
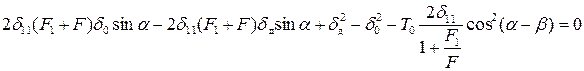 .
.
Учитывая, что 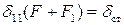 – статическое перемещение (перемещение точки соударения под действием силы тяжести взаимодействующих тел, приложенной статически по направлению перемещения во время ударного взаимодействия):
– статическое перемещение (перемещение точки соударения под действием силы тяжести взаимодействующих тел, приложенной статически по направлению перемещения во время ударного взаимодействия):
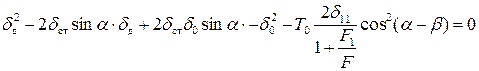 .
.
Поскольку корни квадратного уравнения вида 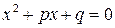 равны
равны 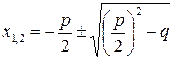 , то
, то
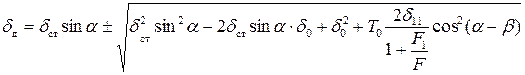 ,
,
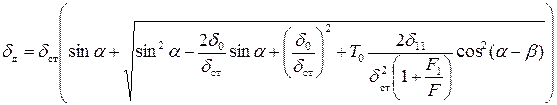 .
.
Таким образом, перемещение при ударе вычисляется по формуле:
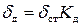 , (4.6)
, (4.6)
где K д – коэффициент динамичности:
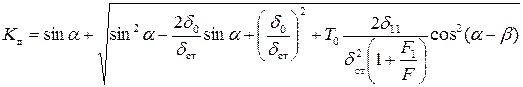 (4.7)
(4.7)
В области упругих деформаций напряжение, возникающее при ударе
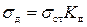 . (4.8)
. (4.8)