
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Класс явно-сократимых КА.
|
|
Автомат называют явно-сократимым, если при его представлении таблицей переходов/выходов найдется по крайней мере одна пара строк (si, sj), которые одинаковы как подтаблице выходов y(t), так и в подтаблице переходов s(t+1).
Это означает, что состояния si и sj –эквивалентные, и автомат может быть минимизирован (сокращен), во всяком случае, удалением одного из них.
Пример. КА задан таблицей переходов/выходов (рис. 5.1):
| y(t) | s(t+1) | ||||||
 x(t)
s(t) x(t)
s(t)
| a | b | c | a | b | c | |
| s0 | s0 | s1 | s3 | ||||
| s1 | s1 | s2 | s3 | ||||
| s2 | s3 | s1 | s0 | ||||
| s3 | s1 | s2 | s3 | ||||
Рис. 5.1. Таблица переходов/выходов исходного КА
Здесь X= {a, b, c}; Y = {0, 1}; S = {s0, s1, s2, s3}.
Очевидно совпадение строк s1 и s3, следовательно, автомат относится к классу явно-сократимых. Поведение автомата одинаково в обоих состояниях при всех входных воздействиях. Одно из состояний (например, s3) можно сократить. Соответствующая ему строка удаляется из таблицы, в подтаблице переходов s3 заменяется на s1 (рис. 5.2):
| y(t) | s(t+1) | ||||||
 x(t)
s(t) x(t)
s(t)
| a | b | c | a | b | c | |
| s0 | s0 | s1 | s1 | ||||
| s1 | s1 | s2 | s1 | ||||
| s2 | s1 | s1 | s0 | ||||
Рис. 5.2. Таблица переходов/выходов КА после сокращения состояния s3.
Одинаковых строк больше нет. Рассмотрим графы переходов исходного и сокращенного автоматов (рис. 5.3):
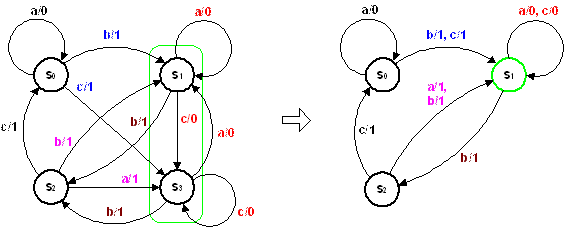
Рис. 5.3. Графы переходов исходного и сокращенного КА.
Видно, что дуги, инцидентные s1, приобрели кратный вес. Например, в графе исходного КА из вершины s0 выходит дуга в s1 с весом b/1 и в s3 с весом c/1. Поэтому дуга s0 ® s1 графа сокращенного КА имеет вес (b/1, c/1). Аналогична ситуация с дугой s2 ® s1 полученного графа. Кроме того, в вершину s2 из вершин s1 и s3 в исходном графе ведут дуги с одинаковыми весами b/1. Поэтому дуга s1 ® s2 графа сокращенного КА приобретает вес b/1. Вершины s1 и s3 исходного графа связаны парными дугами с весами c/0 и a/0. Кроме того, каждая из этих вершин имеет петлю с весом a/0 и c/0 соответственно. Поэтому вершине s1 графа сокращенного КА инцидентна петля с двойным весом (a/0, c/0). Веса дуг исходного и результирующего графов в перечисленных случаях на рис. 5.3 выделены одинаковыми цветами.
Отметим, что полученный КА принадлежит классу явно-минимальных. ▄
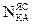 |
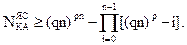 Лемма. Мощность множества явно-сократимых автоматов удовлетворяет неравенству:
Лемма. Мощность множества явно-сократимых автоматов удовлетворяет неравенству:
Пояснение. Ранее было показано, что (qn)pn = NКА. Оценка количества КА с попарно различными строками в таблицах переходов/выходов Ndif может быть выражена неравенством:
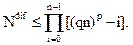 |
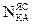 В таком случае формула для становится понятной. ▄
В таком случае формула для становится понятной. ▄