
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема 7. Минимальная форма автомата.
|
|
Пусть А – автомат с m классами эквивалентности: Pэкв = {Σ 1, Σ 2, …, Σ m}, m ≤ n, n = |S|. Введем обозначение s(i) для любого состояния, входящего в класс Σ i:
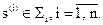 |
Минимальной формой автомата А называют автомат Ã, имеющий m состояний, которые образуют множество:
{s(1), s(2), …, s(m)}.
 Процесс отыскания минимальной формы называют минимизацией автомата. Полученный автомат называют минимальным. Очевидно, минимизация состоит в определении Pэкв и последующем построении характеристических функций автомата Ã с учетом того, что каждый класс в Pэкв – это одно состояние Ã.
Процесс отыскания минимальной формы называют минимизацией автомата. Полученный автомат называют минимальным. Очевидно, минимизация состоит в определении Pэкв и последующем построении характеристических функций автомата Ã с учетом того, что каждый класс в Pэкв – это одно состояние Ã.
Таким образом, индивидуальное распознавание каждого состояния исходного автомата становится ненужным: важно только определить, к какому классу эквивалентности оно относится.
Минимизация автомата может быть выполнена различными способами. Рассмотрим один из возможных – индуктивный алгоритм Мили.
Алгоритм двухэтапный, заключается в поиске пар эквивалентных состояний.
Этап 1, шаг 1. Получение первичного разбиения.
Два состояния si и sj относим к одному классу эквивалентности Σ 1h, если для каждого xk Î X выполняется равенство: fy(si, xk) = fy(sj, xk), т.е. при любом входном воздействии реакция автомата одинакова в обоих состояниях.
Этап 2, шаг (i + 1), i ≥ 1. Итерационное разбиение ранее полученных классов.
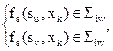 Два состояния su и sv, принадлежащие одному классу эквивалентности Σ ij (индекс i – нумерация шага, индекс j – нумерация класса), относим к классу Σ i+1j, если для каждого xk Î X верно:
Два состояния su и sv, принадлежащие одному классу эквивалентности Σ ij (индекс i – нумерация шага, индекс j – нумерация класса), относим к классу Σ i+1j, если для каждого xk Î X верно:
т.е. под воздействием каждого входного сигнала автомат, находясь как в su, так и в sv, переходит в состояния, принадлежащие одному и тому же классу эквивалентности Σ iw предыдущего разбиения.
Алгоритм завершается при совпадении разбиений на очередном и предыдущем шагах.
Пример. Автомат Мили А задан таблицей переходов/выходов (рис. 7.1). Состояния для краткости обозначены цифрами 1, 2, …, 9. Выполнить минимизацию автомата алгоритмом Мили.
| y(t) | s(t+1) | ||||||
 x(t)
s(t) x(t)
s(t)
| a1 | a2 | a3 | a1 | a2 | a3 | |
Рис. 7.1. Таблица переходов/выходов исходного автомата A.
Шаг 1.
| Вх. / Вых. | s(t) | Вх. / Вых. | s(t) |
| x =a1 / y = 0 | 1, 4, 6, 9 | x =a1 / y = 1 | 2, 3, 5, 7, 8 |
| x =a2 / y = 0 | 2, 3, 8 | x =a2 / y = 1 | 1, 4, 5, 6, 7, 9 |
| x =a3 / y = 0 | 2, 3, 5, 7, 8 | x =a3 / y = 1 | 1, 4, 6, 9 |
В результате первичного разбиения имеем три класса эквивалентности:
Σ 11 = {1, 4, 6, 9}, Σ 12 = {2, 3, 8}, Σ 13 = {5, 7}.
Шаг 2.
 x(t)
s(t) x(t)
s(t)
| s(t+1) |  x(t)
s(t) x(t)
s(t)
| s(t+1) |  x(t)
s(t) x(t)
s(t)
| s(t+1) | |||||||||
| a1 | a2 | a3 | a1 | a2 | a3 | a1 | a2 | a3 | ||||||
| Σ 11 |  Σ 12 Σ 12
|  Σ 11 Σ 11
|  Σ 11 Σ 11
| Σ 12 |  Σ 11 Σ 11
|  Σ 11 Σ 11
|  Σ 13 Σ 13
| Σ 13 |  Σ 11 Σ 11
|  Σ 11 Σ 11
|  Σ 12 Σ 12
| |||
| Σ 12 | Σ 11 | Σ 11 | Σ 11 | Σ 11 | Σ 13 | Σ 11 | Σ 11 | Σ 12 | ||||||
| Σ 12 | Σ 11 | Σ 11 | Σ 11 | Σ 11 | Σ 13 | |||||||||
| Σ 13 | Σ 11 | Σ 13 |
Пояснение. Последовательно рассматриваем классы, полученные на предыдущем шаге. В текущем классе для каждого состояния и каждого входного сигнала определяем, какому классу предыдущего шага принадлежит состояние, в которое переходит автомат в момент времени t+1.
На шаге 2 получаем разбиение:
Σ 21 = {1, 4, 6}, Σ 22 = {2, 3, 8}, Σ 23 = {5, 7}; состояние 9 выделяется в отдельный класс: {9}.
Шаг 3.
 x(t)
s(t) x(t)
s(t)
| s(t+1) |  x(t)
s(t) x(t)
s(t)
| s(t+1) |  x(t)
s(t) x(t)
s(t)
| s(t+1) | |||||||||
| a1 | a2 | a3 | a1 | a2 | a3 | a1 | a2 | a3 | ||||||
| Σ 21 |  Σ 22 Σ 22
|  Σ 21 Σ 21
|  Σ 21 Σ 21
| Σ 22 |  Σ 21 Σ 21
|  Σ 21 Σ 21
|  Σ 23 Σ 23
| Σ 23 |  Σ 21 Σ 21
|  Σ 21 Σ 21
|  Σ 22 Σ 22
| |||
| Σ 22 | Σ 21 | Σ 21 | Σ 21 | Σ 21 | Σ 23 | Σ 21 | Σ 21 | Σ 22 | ||||||
| Σ 22 | {9} | Σ 21 | Σ 21 | Σ 21 | Σ 23 |
Результат шага 3: Σ 31 = {1, 4}, Σ 32 = {2, 3, 8}, Σ 33 = {5, 7}; {6}, {9}.
Шаг 4.
 x(t)
s(t) x(t)
s(t)
| s(t+1) |  x(t)
s(t) x(t)
s(t)
| s(t+1) |  x(t)
s(t) x(t)
s(t)
| s(t+1) | |||||||||
| a1 | a2 | a3 | a1 | a2 | a3 | a1 | a2 | a3 | ||||||
| Σ 31 |  Σ 32 Σ 32
|  Σ 31 Σ 31
|  Σ 31 Σ 31
| Σ 32 |  2 2
|   Σ 31 Σ 31
|   Σ 31 Σ 31
|  Σ 33 Σ 33
| Σ 33 |  {6} {6}
|  Σ 31 Σ 31
|  Σ 32 Σ 32
| ||
| Σ 32 | Σ 31 | Σ 31 | Σ 31 | {6} | Σ 33 | {6} | Σ 31 | Σ 32 | ||||||
 Σ 31 Σ 31
|  Σ 31 Σ 31
|  Σ 33 Σ 33
|
Результат шага 4: Σ 41 = {1, 4}, Σ 42 = {2, 8}, Σ 43 = {5, 7}; {3}, {6}, {9}.
Шаг 5.
 x(t)
s(t) x(t)
s(t)
| s(t+1) |  x(t)
s(t) x(t)
s(t)
| s(t+1) |  x(t)
s(t) x(t)
s(t)
| s(t+1) | |||||||||
| a1 | a2 | a3 | a1 | a2 | a3 | a1 | a2 | a3 | ||||||
| Σ 41 |  Σ 42 Σ 42
|  Σ 41 Σ 41
|  Σ 41 Σ 41
| Σ 42 |  Σ 41 Σ 41
|  Σ 41 Σ 41
|  Σ 43 Σ 43
| Σ 43 |  {6} {6}
|  Σ 41 Σ 41
|  {3} {3}
| |||
| Σ 42 | Σ 41 | Σ 41 | Σ 41 | Σ 41 | Σ 43 | {6} | Σ 41 | {3} |
Результат шага 5: Σ 51 = {1, 4}, Σ 52 = {2, 8}, Σ 53 = {5, 7}; {3}, {6}, {9} – совпадает с разбиением на шаге 4. Конец итераций.
Получены шесть классов эквивалентности: следовательно, автомат в минимальной форме имеет шесть состояний. Введем обозначения:
s(1) = {1, 4}, s(2) = {2, 8}, s(3) = {3}, s(4) = {5, 7}, s(5) = {6}, s(6) = {9}.
Таблица переходов/выходов минимального автомата Ã имеет вид, показанный на рис. 7.2.
| y(t) | s(t+1) | ||||||
 x(t)
s(t) x(t)
s(t)
| a1 | a2 | a3 | a1 | a2 | a3 | |
| s(1) | s(2) | s(1) | s(1) | ||||
| s(2) | s(1) | s(1) | s(4) | ||||
| s(3) | s(1) | s(5) | s(4) | ||||
| s(4) | s(5) | s(1) | s(3) | ||||
| s(5) | s(2) | s(6) | s(5) | ||||
| s(6) | s(4) | s(6) | s(4) | ||||
Рис. 7.2. Таблица переходов/выходов минимального автомата Ã.
Фрагменты графов автоматов A и Ã представлены на рис. 7.3. Соответствия вершин показаны пунктиром.
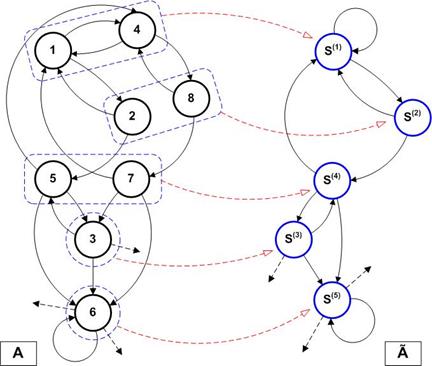 |
Рис. 7.3. Фрагменты графов исходного и минимального автоматов.
Читателю предлагается самостоятельно проанализировать оба графа, сопоставить две картины инцидентности дуг вершинам, проставить веса дуг и убедиться в функциональной эквивалентности минимального и исходного автоматов.
Контрольные вопросы.
1. Что такое класс конечных автоматов?
2. Какие автоматы относят к классу явно-минимальных? Явно-сократимых?
3. Какие конечные автоматы называют изоморфными?
4. Что такое эквивалентные состояния конечного автомата? Каковы их свойства?
5. Что такое эквивалентное разбиение конечного автомата?
6. Что называют минимальной формой автомата?
7. В чем состоит итерационный алгоритм Мили отыскания минимальной формы автомата?