Тема 6. Эквивалентные состояния автомата и их свойства.

Рассмотрим следующую модель. Автомат А последовательно находится в различных состояниях s_i и s_j. И в том, и в другом случае на вход автомата подается входной сигнал x, на выходе формируется сигнал y (рис. 6.1). Возможно ли отличить состояния s_i и s_j одно от другого? Вопрос разрешается при введении понятия эквивалентных состояний КА, о которых ранее уже упоминалось.

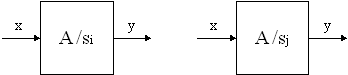
Рис. 6.1. Модель КА в двух различных состояниях.

Введем некоторые базовые определения.

Определение 1. Два состояния s_i и s_j автомата А называются 1-эквивалентными, если при подаче на вход автомата одного и того же входного сигнала x реакция автомата, т.е. выходной сигнал y, будет одной и той же независимо от того, находится ли А в состоянии s_i или в состоянии s_j.

Определение 2. Два состояния s_i и s_j автомата А называются 1-различимыми, если при подаче на вход автомата одного и того же входного сигнала x реакция автомата (y) будет разной в зависимости от того, находится А в состоянии s_i или в состоянии s_j.

Определение 3. Два состояния s_i и s_j автомата А называются k-эквивалентными, если при воздействии на автомат одной и той же последовательностью входных сигналов длиной k автомат выдает одну и ту же выходную последовательность независимо от того, находится ли А в состоянии s_i или в состоянии s_j.

Определение 4. Два состояния s_i и s_j автомата А называются k-различимыми, если при воздействии на автомат одной и той же последовательностью входных сигналов длиной k реакция автомата будет представлять собой различные выходные последовательности в зависимости от того, находится А в состоянии s_i или в состоянии s_j.

Определение 5. Два состояния s_i и s_j автомата А называются (просто) эквивалентными, если при воздействии на автомат одной и той же произвольной последовательностью входных сигналов из множества X реакция автомата будет одинаковой вне зависимости от того, в каком состоянии находится автомат – s_i или s_j.

Определение 6. Два состояния s_i и s_j автомата А называются (просто) различимыми, если при воздействии на автомат одной и той же произвольной последовательностью входных сигналов из множества X реакция автомата будет различной в зависимости от того, в каком состоянии находится автомат – s_i или s_j.

Примечание. В контексте определений 1 – 6 можно говорить об эквивалентности или различимости состояний s_i и s_j разных автоматов, т.е. когда s_i Î S₁, s_j Î S₂, где S₁ и S₂, – множества состояний автоматов A₁ и A₂ соответственно.

Рассмотрим свойства эквивалентных состояний и продолжим ряд определений.

Свойство 1 (лемма). Если два состояния КА являются k-эквивалентными, то они будут и m-эквивалентными для каждого m £ k.

Доказательство. От противного. Пусть состояния КА s_i и s_j k-эквивалентны, но m‑ различимы (m £ k). Тогда существует входная последовательность длиной m, на которой s_i отличается от s_j. Но в таком случае s_i и s_j будут различимы и при входной последовательности длиной k, т.е. s_i и s_j являются k-различимыми, что противоречит условию леммы. Следовательно, предположение неверно, и s_i и s_j m-эквивалентны. ▄

Свойство 2 (лемма). Если два состояния КА являются k-различимыми, то они будут и m‑ различимыми для каждого m ³ k.

Доказательство. Аналогично предыдущему или по свойству 1: пусть s_i и s_j k‑ различимы, но m-эквивалентны (m ³ k). Однако на основании свойства 1, если два состояния m-эквивалентны, то они должны быть и k-эквивалентны, так как k £ m. Полученное противоречие доказывает справедливость леммы. ▄

Определение 7. Состояние, в которое переходит КА из состояния s_i при подаче входной последовательности длиной k, называют k-тым преемником s_i по отношению к данной входной последовательности.

В частном случае, нулевым преемником состояния s_i является само s_i.

Представляет интерес так называемое разбиение множества состояний КА на классы по следующим правилам:

1) все состояния, принадлежащие одному классу, должны быть k-эквивалентными;

2) все состояния, принадлежащие разным классам, должны быть k-различимыми.

Определение 8. Разбиение множества S состояний КА на классы в соответствии с правилами 1) и 2) называется k-эквивалентным разбиением автомата и обозначается P_k.

Определение 9. Классы k-эквивалентного разбиения автомата называются классами k‑ эквивалентности и обозначаются Σ _k1, Σ _k2, …

Определение 10. Состояния КА, принадлежащие одному и тому же классу k‑ эквивалентности Σ _ki, называются смежными, а принадлежащие разным классам – разобщенными.

Замечание. Ни одно из состояний КА не может принадлежать одновременно двум разным классам k-эквивалентности, так как это означало бы k-различимость состояния самому себе. Следовательно, суммарное число состояний в k-эквивалентном разбиении P_k равно мощности множества состояний КА:

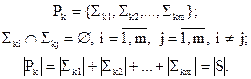Свойство 3 (лемма). k-эквивалентное разбиение автомата единственно.

Доказательство. От противного. Пусть k-эквивалентное разбиение P_k состоит из классов k‑ эквивалентности:

P_k = {Σ _k1, Σ _k2, …, Σ _km}.

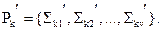Пусть P_k не единственно. Тогда существует другое, альтернативное k-эквивалентное разбиение P_k^’ того же автомата:

Пусть Σ _kj Î P_k, Σ _kj = {s_j1, s_j2, …, s_jd}.

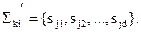Так как каждое состояние, входящее в Σ _kj, k‑ эквивалентно любому другому состоянию из этого же класса и не существует ни одного состояния вне Σ _kj , которое было бы k-эквивалентно хотя бы одному состоянию в Σ _kj, то в альтернативном разбиении P_k^’ должен быть класс эквивалентности Σ _ki^’, включающий те же состояния, что и Σ _kj, и не содержащий никаких других состояний:

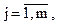Предположив получим, что каждому классу в P_k соответствует идентичный класс в P_k^’. Так как суммарное число состояний в P_k^’ такое же, как в P_k, то

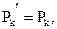то есть k-эквивалентное разбиение автомата является единственным. ▄

Свойство 4 (лемма). Состояния КА, являющиеся разобщенными в P_k, должны быть разобщенными и в (k+1)-эквивалентном разбиении P_k+1.

Доказательство следует из свойства 2.

Свойство 5 (лемма). Если КА имеет два различимых, но k-эквивалентных состояния, то он также имеет два состояния k-эквивалентных, но (k+1)-различимых.

Доказательство: из свойства 2.

Определение 11. k-эквивалентное разбиение автомата А называется (просто) эквивалент­ным разбиением, если во всех классах этого разбиения смежные состояния эквивалентны.

Обозначение: P_экв.

Определение 12. Каждый класс, входящий в эквивалентное разбиение, называется классом эквивалентности.

Обозначение: Σ ₁, Σ ₂, …

Таким образом, P_экв = {Σ ₁, Σ ₂, …, Σ _m}. Эквивалентное разбиение является наиболее детальным разбиением автомата. Оно может быть получено итерационно путем построения k-эквивалентных разбиений при k = 1, 2, 3 и т.д. При совпадении очередного разбиения P_i с предыдущим P_i-1 имеем P_экв. Очевидно, для эквивалентного разбиения автомата с n состояниями потребуется не более (n-1) итерации.

Примечание. Понятия эквивалентных состояний и эквивалентного разбиения позволяют ввести понятие эквивалентных автоматов. Два автомата А₁ и А₂ называют эквивалентными, если каждому состоянию s_i автомата А₁ соответствует, по крайней мере, одно эквивалентное ему состояние автомата А₂ и, обратно, каждому состоянию s_j автомата А₂ сопоставимо хотя бы одно эквивалентное ему состояние автомата А₁. В противном случае автоматы А₁ и А₂ называют различимыми.