
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Изоморфные автоматы.
|
|
Конечные автоматы, характеристические функции которых одинаковы, называются изоморфными друг другу. Это означает, что если некоторая система представлена автоматом А, то любой автомат, изоморфный А, также может служить представлением этой системы. Из сказанного следует, что представление любой системы автоматом не является единственным.
Пусть А – конечный автомат, заданный таблицей переходов/выходов. Если в подтаблице переходов выполнить перестановку символов s1, s2, … sn, то полученная таблица (в подтаблице выходов ничего не меняется) задаст автомат, изоморфный А. Множество различных КА, полученных в результате всех возможных n! таких перестановок, называют семейством перестановок автомата А.
Лемма. Мощность множества перестановок явно-минимального КА с n состояниями равна n!.
Доказательство. Согласно определению явно-минимального автомата, строки в подтаблице y(t) различны. Они остаются различными и после перестановки обозначений состояний. Следовательно, таблицы переходов/выходов, получаемые в результате различных перестановок, различны. Так как строк в таблице n, то число различных перестановок равно n!. ▄
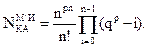 Теорема. Мощность класса минимальных КА, не содержащих изоморфных автоматов, определяется формулой:
Теорема. Мощность класса минимальных КА, не содержащих изоморфных автоматов, определяется формулой:
Доказательство. Множество явно-минимальных автоматов представляет собой объединение семейств перестановок всех автоматов класса, определенного в формулировке теоремы. Так как эти семейства непересекающиеся и, согласно лемме, в каждом семействе ровно n! различных автоматов, то имеет место равенство:
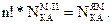
Следовательно,
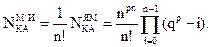 |
▄
Примечание. Понятие изоморфизма автоматов допускает следующую интерпретацию: два автомата изоморфны, если изоморфны их графы переходов.