
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
|
|
Глоссарий (краткий словарь терминов)
| Автомат | Математическая модель системы, обеспечивающей приём, хранение и обработку информации |
| Алгебраическая форма к.ч. | Запись комплексного числа z в виде x + yi называется алгебраической формой комплексного числа. |
| Аналитическая функция | Функция, которая совпадает со своим рядом Тейлора в окрестности любой точки области определения. В случае функции комплексного переменного это свойство совпадает со свойством голоморфности. |
| Аппроксимация | или приближение — замена одних математических объектов другими, в том или ином смысле близкими к исходным. |
| Вычет функции | Вычетом функции f (z) в a называется число
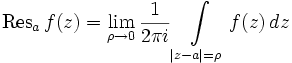 . .
|
| Гармоническая функция | Вещественная функция U, непрерывно дифференцируемая в области D, удовлетворяющая уравнению Лапласа: Δ U = 0, где 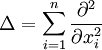 – сумма вторых производных по всем переменным. – сумма вторых производных по всем переменным.
|
| Граф | Граф или неориентированный граф G — это упорядоченная пара G: = (V, E), для которой выполнены следующие условия: V это множество вершин или узлов, E это множество пар (неупорядоченных) различных вершин, называемых рёбрами. |
| Дизъюнкция | двух логических высказываний — логическое высказывание, истинное только тогда, когда хотя бы одно из них истинно. |
| Интерполирование | См. Экстраполирование. |
| Инцидентность | Если v 1, v 2 — вершины, а e = (v 1, v 2) — соединяющее их ребро, тогда вершина v 1 и ребро e инцидентны, вершина v 2 и ребро e тоже инцидентны. |
| Квадратурные формулы | Формулы для оценки значения интеграла. |
| Комплексная функция | Функция которую можно представить в виде
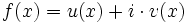 ,
где i — это мнимая единица, т. е. ,
где i — это мнимая единица, т. е. 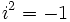 , а , а 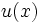 и и  — действительные функции. Функция — действительные функции. Функция 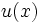 называется действительной частью функции называется действительной частью функции 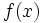 , а , а  — её мнимой частью. — её мнимой частью.
|
| Комплексное число | Любое комплексное число может быть представлено как формальная сумма x + iy, где x и y — вещественные числа, i — мнимая единица, то есть одно из чисел, удовлетворяющих уравнению i 2 = - 1. |
| Конъюнкция | двух логических высказываний — логическое высказывание, истинное только тогда, когда они одновременно истинны. |
| Логическое высказывание | Утверждение, которому всегда можно поставить в соответствие одно из двух логических значений: ложь (0, ложно, false) или истина (1, истинно, truth). Логическое высказывание принято обозначать заглавными латинскими буквами. |
| Маршрут | В графе — это чередующаяся последовательность вершин и рёбер v 0, e 1, v 1, e 2, v 2,..., ek, vk, в которой любые два соседних элемента инцидентны. Если v 0 = vk, то маршрут замкнут, иначе открыт. |
| Матрица инцидентности | Это матрица, значения элементов которой характеризуются инцидентностью соответствующих вершин графа (по вертикали) и его рёбер (по горизонтали). Для неориентированного графа элемент принимает значение 1, если соответсвующие ему вершина и ребро инцидентны. Для ориентированного графа элемент принимает значение 1, если инцидентная вершина является началом ребра, значение -1, если инцидентная вершина является концом ребра. В остальных случаях (в том числе и для петель) значению элемента присваивается 0. |
| Матрица смежности | Это матрица, значения элементов которой характеризуются смежностью вершин графа. При этом значению элемента матрицы присваивается количество рёбер, которые соединяют соответствующие вершины (т.е. которые инцидентны обоим вершинам). Петля считается сразу двумя соединениями для вершины, т.е. к значению элемента матрицы в таком случае следует прибавлять 2. |
| Орграф | Ориентированный граф (сокращенно орграф) G — это упорядоченная пара G: = (V, A), для которой выполнены следующие условия: V это множество вершин или узлов, A это множество (упорядоченных) пар различных вершин, называемых дугами или ориентированными рёбрами. |
| Остаточный член | Разность между заданной функцией и функцией, её аппроксимирующей. Тем самым, оценка остаточного члена является оценкой точности рассматриваемой аппроксимации. |
| Отрицание | Логическое высказывание, принимающее значение " истинно", если исходное высказывание ложно, и наоборот. |
| Первообразная | Первообразной функцией данной функции f называют такую функцию F, производная которой равна f, то есть F ′ = f. |
| Погрешность | Всякое измерение дает результат, лишь приближенный к истинному значению определяемой величины. За истинное значение принимается среднестатическое значение, полученное в результате серии измерений. Но утверждать, что усредненное значение истинно — мы не можем. Поэтому необходимо указать, какова точность измерения. Для этого вместе с полученным результатом указывается погрешность измерений. |
| Подграф | Граф, содержащий некое подмножество вершин данного графа и все рёбра, инцидентные данному подмножеству. |
| Разности конечные | Конечные разности применяются в интерполяционном методе Ньютона |
| Регулярная (голоморфная) функция | Комплекснозначная функция, определённая на открытом подмножестве комплексной плоскости 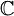 и имеющая непрерывную комплексную производную. Иначе, комплексная функция u + iv = f (x + iy) является регулярной тогда и только тогда, когда выполняются условия Коши — Римана и имеющая непрерывную комплексную производную. Иначе, комплексная функция u + iv = f (x + iy) является регулярной тогда и только тогда, когда выполняются условия Коши — Римана
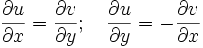 и частные производные
и частные производные 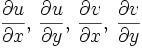 непрерывны. непрерывны.
|
| Ряд Лорана | Двусторонне бесконечный степенной ряд по целым степеням (z − a), то есть ряд вида
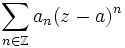
|
| Ряд Тэйлора | Разложение функции в бесконечную сумму степенных функций. Пусть функция f (x) бесконечно дифференцируема в некоторой окрестности точки 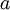 , тогда ряд , тогда ряд
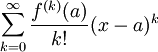 называется рядом Тейлора функции f в точке a.
называется рядом Тейлора функции f в точке a.
|
| Связность | Две вершины в графе связаны, если существует соединяющая их (простая) цепь. |
| Теория графов | Раздел дискретной математики, изучающий свойства графов. В наиболее общем смысле граф можно представить себе как множество вершин (узлов), соединённых рёбрами. |
| Тригонометрическая форма к.ч. | Если вещественную x и мнимую y части комплексного числа выразить через модуль r = | z | и аргумент 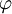 ( (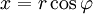 , , 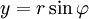 ), то комплексное число z можнозаписать в тригонометрической форме и показательной формах ), то комплексное число z можнозаписать в тригонометрической форме и показательной формах
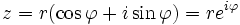 . .
|
| Узлы интерполяции | Пусть имеется n значений xi, каждому из которых соответствует своё значение yi. Требуется найти такую функцию F, что:
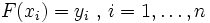 При этом:
При этом:
|
| Условия Коши – Римана | Условия на вещественную u = u (x, y) и мнимую v = v (x, y) части функции комплексного переменного 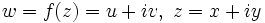 , обеспечивающие дифференцируемость f (z) как функции комплексного переменного. , обеспечивающие дифференцируемость f (z) как функции комплексного переменного.
|
| Формула Симпсона | относится к приемам численного интегрирования. Подынтегральную функцию приближенно заменяют параболами. Для этого отрезок, по которому ведется интегрирование, разбивают на пары отрезков, в каждой из которых по трем точкам строят полином второй степени. |
| Цепь | В графе — маршрут, все рёбра которого различны. Если все вершины (а тем самым и рёбра) различны, то такая цепь называется простой. В цепи v 0, e 1,..., ek, vk вершины v 0 и vk называются концами цепи. Цепь с концами u и v соединяет вершины u и v. Цепь, соединяющая вершины u и v обозначается 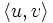 . Для орграфов цепь называется путём. . Для орграфов цепь называется путём.
|
| Эквивалентность | двух логических высказываний — логическое высказывание, истинное только тогда, когда они одновременно истинны или ложны. |
| Экстраполирование | Интерполяционную формулу 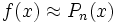 часто используют для приближённого вычисления значений функции f при значениях аргумента x, отличных от узлов интерполирования. При этом различают интерполирование, когда часто используют для приближённого вычисления значений функции f при значениях аргумента x, отличных от узлов интерполирования. При этом различают интерполирование, когда 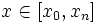 , и экстраполирование, когда , и экстраполирование, когда 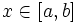 , , 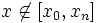 . .
|
Данная страница нарушает авторские права?