Итоговый контроль

Вопросы для подготовки к экзамену

1. Определение абсолютной и относительной погрешности.

2. Постановка задачи интерполяции функции.

3. Конечные разности и интерполяционный многочлен Ньютона.

4. Приближённое вычисление определённого интеграла. Формулы прямоугольников, трапеции, Симпсона.

5. Метод наименьших квадратов.

6. Линейная аппроксимация и линеаризация.

7. Этапы вычисления корней уравнения .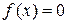

8. Постановка задачи Коши и её решение методом Эйлера.

9. Алгебраическая и тригонометрическая форма комплексного числа.

10. Условия Коши-Римана.

11. Формулы для вычисления производной от функции комплексного переменного.

12. Регулярные и гармонические функции.

13. Геометрический смысл производной от функции комплексного переменного.

14. Равенство Эйлера и выражения тригонометрических функций вещественной переменной через показательную функцию.

15. Интеграл от функции комплексного переменного и его выражение через вещественные криволинейные интегралы.

16. Теорема Коши и регулярность функции комплексного переменного.

17. Основная формула интегрального исчисления для функций комплексного переменного.

18. Интегральная формула Коши.

19. Функциональные ряды. Сходимость и абсолютная сходимость.

20. Ряд Тейлора и теорема Абеля.

21. Ряд Лорана и его сходимость.

22. Изолированные особые точки и их типы.

23. Разложение в ряд Лорана в окрестности бесконечно удалённой точки.

24. Теорема Коши о вычетах.

25. Вычисление вычетов в полюсах первого и второго порядков.

26. Вычет в бесконечно удалённой точке. Основная теорема о вычетах.

27. Дать определения вершин и рёбер графа, графа и орграфа, пути и цикла, полного и неполного графа, связанного и несвязанного графа, дерева и корня дерева.

28. Задача о минимальном пути и алгоритм Дейкстры.

29. Минимальное остовное дерево и алгоритм ближайшего соседа.

30. Формальный язык: состояние, алфавит и правила грамматики.

31. Дискретные автоматы. Комбинационная и последовательная схемы.

32. Сумматор.

33. Операции высказывания, отрицания, конъюнкции, дизъюнкции и эквиваленции. Таблицы истинности для них.

34. Булевы функции и нормальные формы. Правила построения СДНФ и СКНФ.

35. Построение сокращённой ДНФ методом Квайна.

36. Построение минимальной ДНФ методом Петрика.

37. Контактная схема и её логическая функция. Прямая и обратная задачи.

Содержание

Стр.

1. Информация о дисциплине …………………………………………… 3

1.1. Предисловие ……………………………………………………… 3

1.2. Содержание дисциплины и виды учебной работы …………….. 4

2. Рабочие учебные материалы …………………………………………. 6

2.1. Рабочая программа ……………………………………………….. 6

2.2. Тематический план дисциплины ……………………………………... 10

2.3. Структурно-логическая схема дисциплины ……………………. 13

2.4. Временной график изучения дисциплины ……………………… 14

2.5. Практический блок ……………………………………………….. 14

2.6. Балльно-рейтинговая система оценки знаний ………………….. 16

3. Информационные ресурсы дисциплины ……………………………. 17

3.1. Библиографический список ……………………………………… 17

3.2. Опорный конспект лекций по дисциплине ………………… 18

Введение …………………………………………………………. 18

Раздел 1. ЧИСЛЕННЫЕ МЕТОДЫ ………………………………… 18

1.1. Обработка результатов измерений и погрешности вычислений 19

1.2. Интерполяция и численное дифференцирование ……………… 22

1.3. Численное интегрирование ……………………………………… 28

1.4. Приближение функций ………………………………………….. 30

1.5. Многомерные задачи …………………………………………….. 32

1.6. Численные методы алгебры …………………………………….. 33

1.7. Решение систем нелинейных уравнений и задачи оптимизации.. 37

1.8. Численные методы решения обыкновенных дифференциальных уравнений ……………………………………………………………… 37

Раздел 2. ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО

ПЕРЕМЕННОГО …………………………………………….. 40

2.1. Комплексные числа и операции с ними ………………………….. 40

2.2. Функции комплексного переменного (ФКП).

Условия Коши-Римана ………………………………………………… 42

2.3. Элементарные функции и конформные отображения …………… 43

2.4. Представление регулярных функций интегралами ……………….. 45

2.5. Представление регулярных функций рядами ……………………… 49

2.6. Вычеты функций …………………………………………………….. 55

Раздел 3. ДИСКРЕТНАЯ МАТЕМАТИКА …………………………….. 59

3.1. Элементы теории графов ……………………………………………. 60

3.2. Формальные языки и дискретные автоматы ………………………. 64

3.3. Элементы алгебры логики ………………………………………….. 68

3.3. Учебное пособие …………………………………………………… 79

3.4. Глоссарий (краткий словарь терминов) …………………………… 79

3.5. Методические указания к проведению лабораторных работ …….. 83

Лабораторная работа №1 ………………………………………………… 83

Лабораторная работа №2 ………………………………………………… 89

Лабораторная работа №3 ………………………………………………… 97

Лабораторная работа №4 ………………………………………………… 103

Лабораторная работа №5 ………………………………………………… 112

3.6. Методические указания к проведению практических занятий …… 118

Задание 1………………….……………………………………………….. 118

Задание 2…………………………………………………………………... 121

Задание 3…………………………………………………………………… 124

Задание 4…………………………………………………………………… 128

Задание 5…………………………………………………………………… 130

Задание 6…………………………………………………………………… 132

Задание 7…………………………………………………………………… 134

Задания 8, 9………………………………………………………………… 138

Раздел 4. БЛОК КОНТРОЛЯ ОСВОЕНИЯ ДИСЦИПЛИНЫ ………… 139

4.1. Общие указания ……………………………………………...……… 139

4.2. Задания на контрольные работы …………………………….. …….. 139

4.3. Текущий контроль …….…………………………………………….. 147

4.4. Итоговый контроль …………………………………………………… 154

[1] «Рабочая программа по дисциплине, составленная в соответствии с ГОС, представлена в рубрике Рабочие учебные материалы.

[2] «Тематический план, содержащий информацию о видах отчётности по темам, приведён в рубрике Рабочие учебные материалы.

[3] В первом семестре изучения дисциплины.

[4] Только относящееся к данному курсу " Математика, ч.2".