
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Прямые частного положения на чертеже
|
|
Прямые частного положения - это прямые, лежащие в плоскости, параллельной одной из основных плоскостей проекций.
Среди прямых частного положения есть прямые, занимающие особое положение: они перпендикулярны какой-либо из основных плоскостей проекций и совпадают с проецирующим лучом на эту плоскость. Поэтому их назвали проецирующими прямыми. Различают следующие их разновидности.
1. Горизонтально проецирующие прямые, которые перпендикулярны горизонтальной плоскости проекций (рис. 3.2).

 На чертеже:
На чертеже:
a 
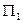
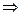 a ||
a || 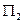 ; a ||
; a || 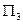 ;
;
a  = a
= a  = a (и.в.)
= a (и.в.)





 a
a  a
a 
a  - главная проекция
- главная проекция
Рис. 3.2
2. Фронтально проецирующие прямые, которые перпендикулярны фронтальной плоскости проекций (рис. 3.3).



 b
b  b
b 
 |
b 
Рис. 3.3
3. Профильно проецирующие прямые, которые перпендикулярны профильной плоскости проекций (рис. 3.4).

 c
c 
c 
 c
c 
Рис. 3.4
Проекция проецирующей прямой на перпендикулярную ей плоскость представляет собой точку. Эту проекцию называют главной проекцией прямой. Она обладает собирательным свойством - является геометрическим местом проекций всех точек этой прямой.
Другие проекции (не главные) совпадают с линиями связи с главной проекцией, составляя с ними угол 0  . Не главные проекции проецирующей прямой равны истинной величине прямой, поскольку прямая параллельна этим плоскостям проекций.
. Не главные проекции проецирующей прямой равны истинной величине прямой, поскольку прямая параллельна этим плоскостям проекций.
Пример (рис. 3.5а). Через т. А провести фронтально проецирующий отрезок АВ длиной 20 мм так, чтобы т. В была бы фронтально невидимой (закрытой).
A  A
A  A
A  = (B
= (B  ) B
) B  A
A 
 | |||
 | |||

 B
B 
|A  B
B  | = |A
| = |A  B
B  | = 20 мм.
| = 20 мм.
A  A
A 
а) дано б) решение
Рис. 3.5.
Все остальные (не проецирующие) прямые, лежащие в плоскостях, параллельных основным плоскостям проекций, называются прямые уровня. Уровень – это положение, когда все точки прямой находятся на одинаковом расстоянии от параллельной ей плоскости проекций. В зависимости от плоскости, которой они параллельны, прямые уровня получили свои персональные названия и обозначения:
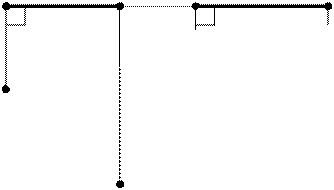
1. Горизонталь (h) – прямая, параллельная горизонтальной плоскости проекций (рис. 3.6).
A  h
h  B
B  A
A  h
h  B
B 



 A
A 
h 
 B
B 
Рис. 3.6
2. Фронталь (f) – прямая линия, параллельная фронтальной плоскости проекций (рис. 3.7).




 B
B  B
B 
f 
 f
f 






 A
A  A
A 
 f
f 



 A
A  B
B 
Рис. 3.7
3. Профильная прямая (p) – прямая, параллельная профильной плоскости проекций (рис. 3.8).






 B
B 
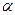 B
B 
 |  |
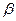

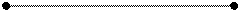 A
A  A
A 
 A
A 




B 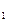

Рис. 3.8
Прямая уровня проецируется на плоскость, которой она параллельна, в натуральную величину. На этой же плоскости без искажения изображаются и углы наклона прямой к другим плоскостям проекций (углы 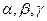 ). Таким образом, метрические задачи по определению длины отрезка и углов наклона к плоскостям проекций прямых уровня – уже решены на чертеже этих прямых. Проекция прямой уровня на плоскость, которой она не параллельна, занимает особое положение: она перпендикулярна линиям связи с параллельной плоскостью проекций. Эту проекцию называют определяющей. Она характеризует прямую уровня, определяет на чертеже её положение в пространстве.
). Таким образом, метрические задачи по определению длины отрезка и углов наклона к плоскостям проекций прямых уровня – уже решены на чертеже этих прямых. Проекция прямой уровня на плоскость, которой она не параллельна, занимает особое положение: она перпендикулярна линиям связи с параллельной плоскостью проекций. Эту проекцию называют определяющей. Она характеризует прямую уровня, определяет на чертеже её положение в пространстве.
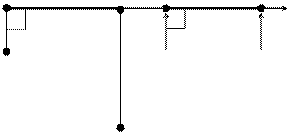
Пример (рис. 3.9а). Через т. А провести горизонталь h под углом 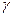 = 60
= 60 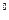 (к плоскости
(к плоскости 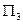 ) так, чтобы прямая h правее т. А располагалась ближе к наблюдателю. Отложить на ней вправо от т. А отрезок АВ длиной 20 мм.
) так, чтобы прямая h правее т. А располагалась ближе к наблюдателю. Отложить на ней вправо от т. А отрезок АВ длиной 20 мм.
A  A
A  A
A  h
h  B
B  A
A  h
h  B
B 
 | |||
 | |||

 A
A  A
A 
 A
A  B
B  = |AB| = 20 мм
= |AB| = 20 мм
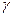

 h
h  B
B 
а) дано б) решение
Рис. 3.9