
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Разновидности плоских поверхностей
|
|
Различают простые и составные плоские поверхности.
Простые плоские поверхности бывают двух видов: плоскости и грани.
Плоскость – неограниченная плоская поверхность. На чертеже плоскость задают изображением элементов её определителя. Плоскость моделируют как траекторию непрерывного перемещения прямой образующей. Перемещение образующей можно задавать следующим образом.
1). Параллельными прямыми – 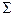 (l, a || b).
(l, a || b).
2). Двумя пересекающимися прямыми – 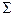 (l, a
(l, a 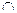 b).
b).
3). Вращением вокруг оси, перпендикулярной образующей
прямой, – 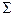 (l
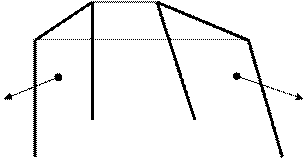
(l  i).
i).
4). Точкой и прямой –  (l, A, b). Этот вариант может быть преобразован в любой из первых трёх.
(l, A, b). Этот вариант может быть преобразован в любой из первых трёх.
Грань – плоскость, ограниченная замкнутой линией. На чертеже
грань изображают линиями её границ (контуром, очерком).
На рис. 5.1 – 5.3 представлены изображения граней: треугольника, четырёхугольника и круга.




 C
C  C
C 
B  B
B 
 |
 A
A  A
A 
Рис. 5.1
 |


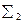
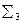
 |
Рис. 5.2
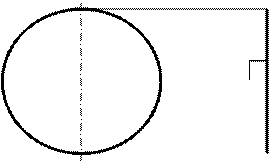 |



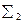
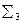
 |
Рис. 5.3
Составные плоские поверхности (многогранные) – представляют собой несколько граней (не лежащих в одной плоскости), состыкованных между собой. Линию стыка каждой пары граней называют рёбром, которое является общей линией границ этих граней (их общей образующей).
Составные плоские поверхности подразделяют на монотипные и комплексные многогранные поверхности.
Монотипные многогранные поверхности моделируют с помощью направляющей ломаной прямой линии. При этом различают следующие варианты таких поверхностей.
1. Призматическая поверхность. Моделирование призматической
поверхности производят путём параллельного перемещения образующей прямой l по направляющей ломаной прямой m (все рёбра между собой параллельны).
На рис. 5.4 представлен аксонометрический чертёж призматической поверхности.







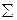


 l
l
 |
 m
m

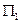
Рис. 5.4
Комплексный чертёж определителя призматической поверхности представлен на рис. 5.5.

 l
l 




 m
m 
 | |||
 |
m 
 |

 l
l 
Рис. 5.5
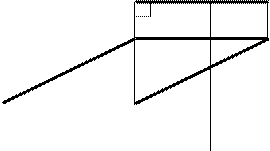
Комплексный чертёж призматической поверхности выполнен на рис. 5.6.
 |

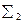
 |
 |

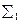
Рис. 5.6
Частным случаем призматической поверхности является призма, которая представляет собой замкнутую призматическую поверхность (направляющая ломаная прямая – замкнута).
На рис. 5.7 приведён чертёж прямой трёхгранной призмы.


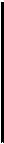







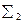
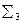
 | |||
 |
Рис. 5.7
2. Пирамидальная поверхность – моделируется перемещением прямой образующей l по ломаной направляющей прямой m, когда другой её конец остаётся в точке S – вершине призматической поверхности (все рёбра пересекаются в одной точке).
На рис. 5.8 представлен комплексный чертёж двухгранной пирамидальной поверхности.


 S
S 


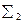 l
l  m
m 







 S
S 






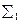
m  l
l 
Рис. 5.8
Частным случаем пирамидальной поверхности является пирамида, которая представляет собой замкнутую пирамидальную поверхность (направляющая ломаная прямая – замкнута).
На рис. 5.9 представлен комплексный чертёж трёхгранной прямой пирамиды.


 S
S 







 S
S 
Рис.5.9
Комплексные многогранные поверхности получают стыковкой граней и многогранных поверхностей разного типа. Примером такой поверхности может служить поверхность октаэдра.