
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение по чертежу взаимного положения прямых линий
|
|
Такое определение связано с решением позиционных и метрических задач.
Прямые линии в пространстве могут занимать одно из следующих трёх возможных взаимных положений:
1. Прямые параллельны.
2. Прямые пересекаются.
2.1. Прямые пересекаются под прямым углом.
3. Прямые скрещиваются.
3.1. Прямые скрещиваются под прямым углом.
1. Определение по чертежу параллельных прямых линий
(позиционные задачи)
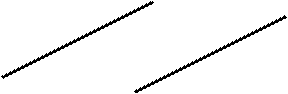
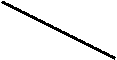
Признак параллельности прямых линий на чертеже (рис. 3.14): одноимённые проекции таких прямых - параллельны.
 |
b  ||a
||a 
 a
a 
 B
B 
 B
B 
 a
a 
b  ||a
||a 
Рис. 3.14
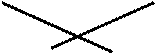
2. Определение по чертежу пересекающихся прямых линий (позиционные задачи)
Признак пересекающихся прямых на чертеже (рис.3.15): точки пересечения одноимённых проекций пересекающихся прямых лежат на одной линии связи, являясь проекциями точки пересечения этих прямых.

 M
M 

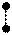 a
a  b
b 
 |
a  M
M  b
b 
Рис. 3.15
2.1. Определение по чертежу перпендикуляно пересекающихся прямых (комплексные задачи)
Определение таких прямых базируется на признаке пересекающихся прямых (позиционная задача) и на свойстве проецирования прямого угла (ОМЗ-2): прямой угол проецируется на плоскость без искажения только в том случае, если хотя бы одна из его сторон параллельна этой плоскости.
Признак перпендикулярно пересекающихся прямых (рис. 3.16):
если одна из перпендикулярно пересекающихся прямых является прямой уровня, то на плоскости проекций, которой она параллельна, прямой угол изображается без искажения.
 b
b 


 A
A  h
h 
 |

 A
A 
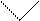 |
b 
h 
Рис. 3.16
3. Определение по чертежу скрещивающихся прямых (позиционные задачи)
Признак скрещивающихся прямых на чертеже (рис. 3.17):
точки пересечения одноимённых проекций скрещивающихся прямых не лежат на одной линии связи, а являются слиянием двух проекций конкурирующих точек этих прямых.
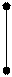

 B
B  = (A
= (A  ) C
) C 
 |
a  D
D 

 a
a  A
A  b
b 
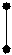
 b
b 
B  C
C  =(D
=(D  )
)
Рис. 3.17
4. Определение по чертежу перпендикулярно скрещивающихся прямых (комплексные задачи).
Признак перпендикулярно скрещивающихся прямых на чертеже (рис. 3.18): если одна из перпендикулярно скрещивающихся прямых параллельна какой-либо плоскости проекций, то на этой плоскости угол между их проекциями остаётся без искажения прямым.
 a
a 
h 
 |

 h
h  a
a 
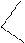 |
Рис. 3.18