Финансовые вычисления в экономике недвижимости.

Простейшим видом финансовой сделки является однократное предоставление в долг некоторой суммы PV с условием, что через некоторое время t будет возвращена б о льшая сумма FV. Как известно, результативность такой сделки может быть оценена двояко: либо с помощью абсолютного показателя – прироста (FV – PV), либо путем расчета некоторого относительного показателя. Абсолютные показатели чаще всего не подходят для подобной оценки ввиду их несопоставимости в пространственно-временном аспекте. Поэтому пользуются специальным коэффициентом – ставкой. Этот показатель рассчитывается отношением приращения исходной суммы к базовой величине, в качестве которой, очевидно, можно взять либо PV, либо FV. Таким образом, ставка может быть рассчитана по одной из двух формул:

темп прироста: 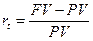, (1)

темп снижения: 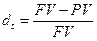. (2)

В финансовых вычислениях первый показатель имеет еще название «процентная ставка», «процент», «рост», «норма прибыли», «доходность». Второй показатель – «учетная ставка», «дисконт». Оба показателя, очевидно, взаимосвязаны:

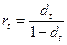или . (3а, 3б)

Капитал, вложенный в недвижимость, увеличивает за год свой размер на величину процента, определяемого ставкой процента. Последняя определяется как отношение чистой прибыли к вложенному капиталу. Рост каждой единицы капитала за период в n лет может определяться либо по правилу простого процента, когда процент начисляют только на первоначальную сумму, либо по правилу сложного процента, когда процент начисляют на всю накопленную к началу года сумму.

Первый способ проще в вычислениях, второй несколько сложнее. Применение первого способа оправдано при незначительной ставке процента и малых периодах накопления:

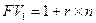. (4)

Применение второго способа объективно правильно, однако опирается на допущение, что вложенные деньги не будут изыматься из оборота до конца срока инвестирования:

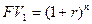. (5)

Выражение (4) носит название формулы простого процента, выражение (5) – формулы сложного процента. Выражение (5) записанное не для единицы, а для всей суммы 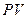капитала:

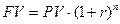(5а)

показывает как возрастает капитал за n периодов при ставке процента r. Если начисление (взимание) процентов производится не один раз в год, а m раз (например при ежемесячном начислении m =12, при ежеквартальном – m =4), то используется формула:

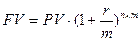. (5б)

Эту формулу можно использовать не только для нахождения суммы, получаемой в результате вложения капитала под процент, или ожидаемой стоимости актива через n лет при известном темпе роста его стоимости r, но и для решения других задач: определение доходности операции по покупке объекта недвижимости с последующей его продажей через определенное время, расчет срока, необходимого для заданного увеличения капитала, вложенного под определенный процент и т.д.

Оценивая целесообразность финансовых вложений в тот или иной актив, исходят из оценки будущих поступлений (в виде процентов, прибыли, дивидендов) с позиции текущего момента. Базовая расчетная формула для такого анализа:

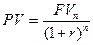, (6)

где: 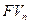- доход, планируемый к получению в n -ом году;

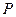- текущая (или приведенная) стоимость, т.е. оценка величины 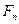с позиции текущего момента;

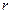- ставка дисконтирования (в эволюционно развивающейся экономике можно использовать ставку доходности).

Многие финансовые операции в экономике недвижимости имеют характер не разовых платежей или поступлений, а представляют собой серии регулярных платежей или поступлений. В качестве примеров таких серий можно привести арендные платежи или платежи в погашение кредитов. Последовательность одинаковых платежей, производимых (или получаемых) через равные промежутки времени, называется аннуитетом.

Формула будущей стоимости аннуитета:

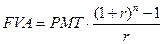, (7)

где: PMT – размер регулярного платежа.

Или, в случае осуществления платежей не один раз в год, а m раз:

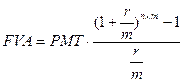. (7а)

Эту формулу также называют фактором фонда накопления капитала, поскольку она показывает накопленную к концу n -го периода денежную сумму при условии вложения в каждом периоде определенной суммы под r процентов.

Иногда необходимо знать какой платеж нужно ежегодно (ежемесячно) вносить, чтобы к концу n-го периода времени накопить заданную сумму. Эта задача может быть решена с использованием формул (7) или (7а) после несложного их преобразования. Такая формула получила название фактор фонда возмещения капитала.

Для расчета текущей стоимости аннуитета используют формулу:

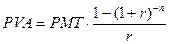, (8)

или, соответственно:

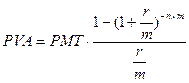. (8а)

С её помощью можно, например, рассчитать текущую (приведенную) стоимость предстоящих арендных платежей или текущую стоимость будущих доходов для целей принятия инвестиционных решений.