
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчет обратной матрицы методом триангуляции
|
|
По определению
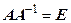
| (4.3) |
Обозначим Х = А -1, а 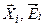 - столбцы матриц, соответственно Х и Е. В этом случае условие (4.3) может быть представлено в блочном виде
- столбцы матриц, соответственно Х и Е. В этом случае условие (4.3) может быть представлено в блочном виде
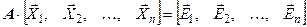 . .
| (4.4) |
Выражение (4.4) определяет n систем линейных уравнений 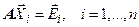 , решение которых определяет искомую обратную матрицу. Многократное решение СЛУ с неизменной матрицей коэффициентов A предопределяет выбор алгоритма – предварительная триангуляция матрицы A:
, решение которых определяет искомую обратную матрицу. Многократное решение СЛУ с неизменной матрицей коэффициентов A предопределяет выбор алгоритма – предварительная триангуляция матрицы A: 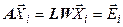 . Решение СЛУ с триангулированной матрицей коэффициентов
. Решение СЛУ с триангулированной матрицей коэффициентов 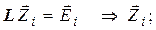
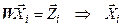 ,
, 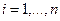
Такой способ получения обратной матрицы требует примерно 2 n 3 операций.
Пример:
Задана матрица
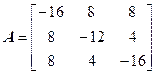 .
.
Методом триангуляции требуется вычислить ее обратную матрицу 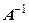 .
.
В результате триангуляции получаем
 ,
, 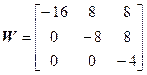 .
.
Вектор  определяется в два этапа. Для первого столбца обратной матрицы
определяется в два этапа. Для первого столбца обратной матрицы
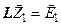 : : 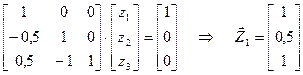 ; ;
| (4.5) |
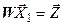
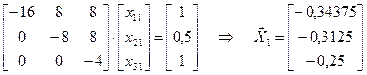 .
.
Аналогично (с заменой в (4.5) 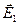 на
на 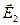 и
и 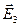 ) определяются
) определяются 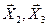 и в целом матрица А - 1 (читателю предлагается выполнить расчеты и проверку самостоятельно).
и в целом матрица А - 1 (читателю предлагается выполнить расчеты и проверку самостоятельно).
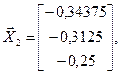
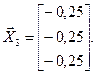
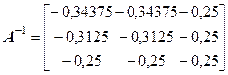 .
.