Применение интерференции. Интерферометры.

Интерференция света используется для технических, но в основном, в измерительных целях. Суть измерений заключается в расшифровке интерференционной картине, которую можно наблюдать как непосредственно (например, при сравнении эталона с поверяемым образцом путем их притирки), так и с помощью специальных оптических устройств - интерферометров, в которых предусмотрены средства для точных измерений параметров этих картин. Интерферометры относятся к числу наиболее точных приборов, поскольку рабочей мерой в них является длина волны, а современные оптико-электронные и цифровые устройства позволяют измерять смещения полос с точностью до сотых долей длины волны.

С помощью интерферометрии можно решить следующие задачи:

-измерять длины, углы и расстояния;

-определять характеристики оптических устройств;

-определять показатели преломлений оптических материалов;

-измерять отступления от плоскостности и параллельности;

-исследовать спектры;

-исследовать химический состав жидкостей, газов и вообще прозрачных материалов;

-и многое другое.

Интерферометры делятся на двулучевые и многолучевые. В первых - распределение освещенности имеет синусоидальный характер. Из-за этого полосы не имеют четких границ и в них наблюдается плавный переход от светлого к темному. В многолучевых - интерференционная картина состоит их узких, резко очерченных полос, поэтому точность определения их положения при прочих равных значительно выше, но конструкция у них сложнее. В настоящем разделе будут рассмотрены лишь двулучевые интерферометры.

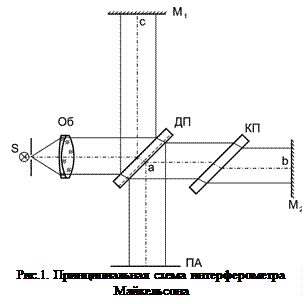Интерферометры типа Майкельсона. К этому типу относится ряд приборов, имеющих схожее устройство, но решающие разные задачи. Принцип действия этих приборов будет понятен из рассмотрения одинаковой для всех них принципиальной схемы.

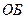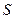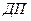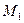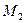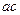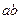Объектив коллимирующей системы преобразует световой поток от источника в параллельный пучок, который попадает на делительную пластину . На дальнюю от источника света сторону пластины нанесено полупрозрачное покрытие. Образованные таким образом два пучка попадают затем на зеркала и , распространяясь по ветвям и . Отразившись от этих зеркал, световые пучки вновь попадают на делитель, где объединяются и распространяясь вместе попадают в плоскость анализа , где и происходит интерференция. Если в ветвях интерферометра поместить разные фазовые объекты, с фазовыми пропусканиями и 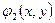, то в соответствии с основным уравнением интерференции (Л13), выражение для распределения освещенности будет иметь вид

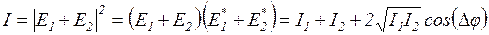
(1)

где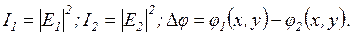

В случае использования немонохроматического источника света незаменимым элементом схемы становится компенсационная пластина КП. Ее роль легко понять из принципа «от противного». Допустим, что пластина КП в схеме отсутствует. В этом случае геометрическая разность хода интерферирующих лучей, за вычетом расстояний, которые они проходят совместно, была бы 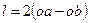. Однако, помимо воздуха, свет распространяется и в стекле делительной пластины, причем в плече 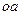свет проходит в стекле в три раза большее расстояние, чем в плече 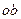благодаря нанесению на одну из сторон пластины полупрозрачного покрытия. В таком случае разность хода будет

(2)

Так как стекла обладают дисперсией , то разность хода 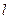в данном случае будет также функцией длины волны и ни при каких вариациях с длинами плеч 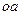и 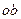она не будет равна нулю для всех длин волн. Полученный результат указывает на невозможность формирования в такой схеме условия возникновения ахроматической полосы – равенства нулю разности хода для всех длин волн. В свою очередь отсутствие такой полосы делает невозможным наблюдения всей интерференционной картины при немонохроматическом источнике света.

Теперь становится понятна роль компенсационной пластины, которая должна быть изготовлена из такого же материала, как и делительная пластина и совпадать с ней по всем размерам, т.е. быть полностью ей эквивалентной. Будучи помещенной в схему, она как раз и скомпенсирует двойной проход света в стекле в плече 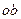. Из сказанного также следует, что в случае использования монохроматического источника (лазера или даже осветителя со светофильтром) компенсационная пластина становится ненужной и ее можно из схемы удалить.

Определим контраст интерференционной картины. Предположим, что коэффициенты отражений у зеркал 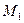и 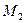одинаковы. Тогда разницу в световых потоках может внести делительная пластина. Пусть ее коэффициент отражения будет 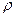, а коэффициент пропускания 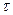. Тогда световой поток, распространяющийся по ветви 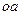после прохождения КП, будет 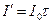, где 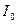- световой поток до КП. После отражения в значение для 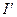добавится множитель 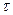, т.е. величина этого потока будет 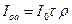. Пучок же идущий по ветви 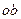сначала отразится от КП, а затем пройдет сквозь нее, и его величина будет 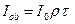, т.е. 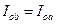при любых значениях коэффициентов пропускания или отражения у КП. Это означает, что контраст интерференционной картины всегда будет равен единице, а изменяться будет лишь освещенность интерференционной картины. Так как 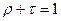, то максимальное значение освещенности в интерференционной картине будет при 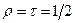, что нетрудно показать, исследуя на максимум выражение .

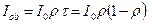Интерферометры типа Майкельсона применяются для многих практических целей. Приведем далеко не полный список задач, решаемых этим прибором:

1. Измерение и контроля двухгранных углов – интерферометр Reflect;

2. Измерение волновых аберраций – интерферометр Тваймана;

3. Измерения чистоты поверхностей - интерферометр Линника;

2. Быстрое определение спектрального состава излучения – Фурье спектрометр.

Рассмотрим каждую из этих схем в отдельности.

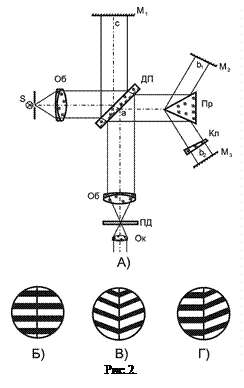
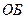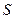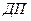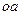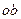Схема Reflect. Для измерения двухгранных углов часто используется интерферометр Reflect. Схема его приведена на рис.2А. Сформированный объективом параллельный пучок от монохроматического источника[1] разделяется делителем на две ветви и . По ветви 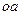свет направляется на зеркало 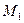, а по 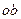на эталонную призму, которая устанавливается на специальной юстировочной площадке между зеркалам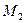и и 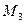так, чтобы интерференционные полосы от обеих граней были симметричны и располагались перпендикулярно ребру двухгранного угла (рис.2Б). Затем на место эталонной призмы устанавливают поверяемую. Из-за случайных неоднородностей, возникших при ее изготовлении, призма на этой площадке также случайным образом и интерференционная картина будет иметь вид, как показано на рис.2В. Затем юстировочными подвижками выставляем верхнюю грань также как и у эталонной, при этом интерференционные полосы будут перпендикулярны ребру призмы (рис.2Г). И, наконец, с помощью клинового компенсатора разворачиваем световой пучок так, чтобы интерференционная картина совпадала с картиной эталонной пластины. При этом значение двугранного угла считывается по шкале, которой снабжен клиновой компенсатор.

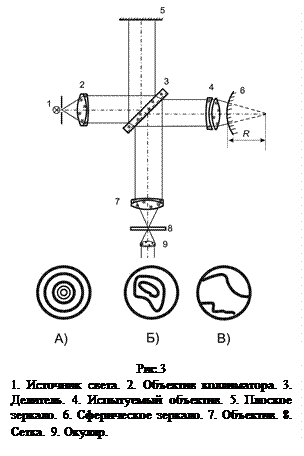Интерферометр Тваймана. Если на объектив, свободный от сферической аберрации, падает плоская волна, распространяющаяся параллельно его оптической оси, то формируемые им сферические волны сходятся в фокусе этого объектива. Если же аберрации присутствуют, то гомоцентричность волны нарушается, т.е. нормали к волновому фронту - лучи уже не пересекаются в точке фокуса. Для определения деформаций этого волнового фронта, т.е. волновой аберрации можно использовать интерферометр Тваймана, схема которого приведена на рис.3 Испытуемый объектив 4 устанавливается в правую ветвь интерферометра. Идущий от источника света 1 световой поток, проходя объектив коллиматора 2, делителем 3 делится на две части. Одна из них отражается от плоского зеркала, а другая проходит через испытуемый объектив 4, отражается от сферического зеркала 5, вторично проходит объектив 4 и отразившись от 3 и пройдя объектив 6 попадает в плоскость полевой диафрагмы, где интерферирует с плоским волновым фронтом, отразившегося от 5.

Так как изначально центр сферического зеркала не совпадает с фокусом объектива, то картина интерференции представляет собой систему колец Ньютона, поскольку из-за несогласованности зеркала и испытуемого объектива правый пучок является практически сферическим, а имеющиеся в нем аберрации много меньше получившейся дефокусировки (рис 3А). Если смещать зеркало относительно объектива, то это уменьшит дефокусировку и приведет к увеличению расстояние между интерференционными кольцами (рис 3Б). Однако окончательно полосы, в случае аберрационного объектива, таким образом устранить не удастся. Картина, при которой расстояние между полосами будет максимально, будет представлять собой сечение волнового фронта перпендикулярными оптической оси плоскостями, отстоящих друга от друга через половину длины волны. Исследуя получившуюся картину можно судить об аберрациях объектива.

Интерферометр Линника. Разработанный в Государственном оптическом институте под руководством В.П. Линника и носящий его имя интерферометр предназначен как для визуального контроля качества полированных поверхностей, так и для измерений различного рода их дефектов, таких как царапины, сколы, заусенцы, неточности обработки, разного рода выступы, «раковины» и т.д. и т.п. Благодаря удачному совмещению в одном приборе микроскопа с большим увеличением и интерферометра типа Майкельсона, прибор позволяет не только увидеть интересующую нас часть поверхности с увеличением, но и провести необходимые трехмерные измерения изображения: в горизонтальной плоскости с помощью окуляр-микрометра, а в вертикальной – анализируя интерференционную картину, появляющуюся на интересующем нас участке объекта. Прибор прост в эксплуатации, имеет ряд приспособлений, позволяющих изменять направление интерференционных полос, а также расстояния между ними. Также имеется возможность фиксировать изображение контролируемой поверхности совместно с интерференционной картиной каким либо фоточувствительным слоем.

Схема прибора приведена на рис 3.1. Световой поток, исходящий из источника 1 с помощью коллимирующего объектива 2 превращается в параллельный пучок, который делителем 3 расщепляется на два – ОА и ОВ. Делитель представляет собой плоскопараллельную пластину, на заднюю часть которой (по отношению к источнику света), нанесено полупрозрачное покрытие. Половина потока распространяется в ветви ОА, строя с помощью микрообъектива 5 на предмете 7 изображение источника света, освещая тем самым те участки предмета, на которых фокусируются элементы тела накала источника. Затем, освещенный таким образом предмет с помощью того же микрообъектива 5 и объектива 9 строит изображение предмета в плоскости полевой диафрагмы (ПД), где расположена шкала.

Второй пучок распространяется аналогично, но по ветви ОВ и освещает участок эталонного зеркала 8, наклоненного под малым углом к оптической оси, который можно изменять. Таким образом, оба пучка попадают в плоскость полевой диафрагмы, где одновременно строят как изображение предмета, так и наклоненного зеркала, образуя из этих изображений оптический виртуальный клин, в котором появляются полосы равной толщины, а на линии пересечения граней образуется ахроматическая полоса, поскольку в этом месте разность хода интерферирующих лучей равна нулю. Этот клин в свою очередь можно считать изображением еще двух клиньев: клина, одной гранью которого является поверхность объекта, а другой гранью – мнимое изображение эталонного зеркала в зеркале, коим является полупрозрачное покрытие делительного кубика (в точке А) и наоборот, когда действительной гранью является эталонное зеркало (в точке В, рис 3.1).

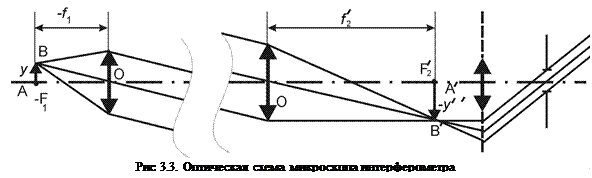
Принципиально, такой метод измерений не отличается от интерференционных измерений в обычном клине с той лишь разницей, что либо одна из граней клина (если его рассматривать между контролируемой поверхностью и мнимым изображением эталонного зеркала), либо обе грани являются виртуальными – т.е. изображениями. У такого клина, как это говорят в оптике, имеется засечка. (Рис 3.2). Это означает, что оптические поверхности как бы проходят сквозь друг друга. Ясно, что с материальными телами такого быть не может. Кроме того, этот клин расположен в плоскости полевой диафрагмы и не составляет проблем измерения его параметров. Обе ветви ОА и ОВ совместно с общим участком от делителя до ПД (рис. 3.1) представляют собой микроскопы с параллельным ходом лучей. Покажем это. Для этого рассмотрим оптическую систему, состоящую из двух линз (объективов) с различными фокусными расстояниями и расположенными на произвольном расстоянии друг от друга. Если поместить предмет в переднем фокусе первой линзы, то изображение сформируется в заднем фокусе второй линзы при любых взаимных положениях линз (рис.3.3). Из построения видно, что треугольники АОВ и А'О'В ' подобны, так как главные лучи ВО и В'О' параллельны, откуда следует выражение для линейного увеличения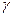

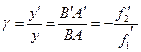
(3.1)

Эта величина может быть весьма значительной и достигать нескольких сотен крат. Подобные схемы микроскопов обладают рядом достоинств и используются в различных приборах и устройствах, например в МБС (микроскоп биологический стереоскопический), в офтальмологических щелевых лампах и многих других.

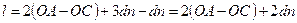
(3.2)

В случае использования немонохроматического источника света незаменимым элементом схемы становится компенсационная пластина 4. Ее роль легко понять из принципа «от противного». Допустим, что пластина 4 в схеме отсутствует. В этом случае геометрическая разность хода интерферирующих лучей, за вычетом расстояний, которые они проходят совместно, была бы 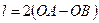. Однако, помимо воздуха, свет распространяется и в стекле делительной пластины, причем в плече ОА свет проходит в стекле в три раза большее расстояние, чем в плече ОВ (рис 3.4) благодаря нанесению на одну из сторон пластины полупрозрачного покрытия. В таком случае разность хода будет

Так как стекла обладают дисперсией , то разность хода 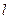в данном случае будет также функцией длины волны и ни при каких вариациях с длинами плеч ОА и ОВ она не будет равна нулю для всех длин волн. Полученный результат указывает на невозможность формирования в такой схеме условия возникновения ахроматической полосы – равенства нулю разности хода для всех длин волн. В свою очередь отсутствие такой полосы делает невозможным наблюдения всей интерференционной картины при немонохроматическом источнике света.

Теперь становится понятна роль компенсационной пластины, которая должна быть изготовлена из такого же материала, как и делительная пластина и совпадать с ней по всем размерам, т.е. быть полностью ей эквивалентной. Будучи внесенной в схему она как раз и скомпенсирует двойной проход света в стекле в плече ОВ. Из сказанного также следует, что в случае использования монохроматического источника (лазера или даже осветителя со светофильтром) компенсационная пластина становится ненужной и ее можно из схемы удалить.

Известно, что в общем виде распределение освещенности в интерференционной картине при интерференции двух пучков определяется выражением

,

(3.3)

где - 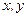- координаты в плоскости интерференционной картины; 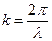-волновое число; распределения освещенности каждого из интерферирующих пучков; 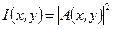- где 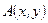комплексная амплитуда каждого из пучков; 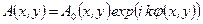- 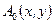распределение амплитуд электромагнитного поля в сечении пучка; 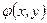- уравнение волновой поверхности в пучке.

В рассматриваемом случае уравнение для волновой поверхности пучка 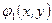, отраженного от исследуемого объекта, поскольку оно является оптической длиной луча, представляет собой удвоенную высоту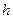

, (3.4)

где 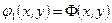уравнение, описывающее форму поверхности.

Выражение для второго пучка есть уравнение плоскости, нормаль которой с оптической осью составляет угол 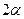(множитель 2 появился из-за отражения). Так как угол весьма мал, то уравнение этой плоскости в системе координат, у которой ось OZ направлена по оптической оси, а ось OY лежит в этой плоскости, будет (рис 3.5)

.

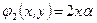(3.5)

Если пучки по сечению имеют равномерные распределения, то 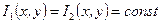и переменная часть распределения освещенности в (3) является аргументом функции cos. Следовательно, все распределение представляет собой пространственную периодическую структуру, т.е. систему полос. Светлые полосы появляются, когда cos= 1, это условия максимума. Минимум же (темные полосы) образуются при таких комбинациях х и у, когда, соответственно cos= -1. Рассмотрим, для определенности, светлые полосы. Они возникают при условии

,

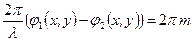(3.6)

где m целое число.Подставляя в (3.7) выражения (3.4) и (3.5) получим

.

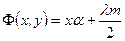(3.7)

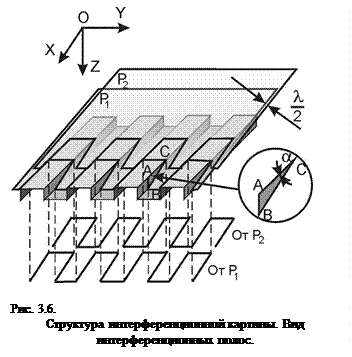Геометрически, выражение (3.7) представляет собой сечения интересующей нас поверхности 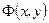рядом наклоненных под углом плоскостей (на рисунке 6 это P₁ и P₂), отстоящих друг от друга на расстоянии 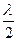. В качестве примера показано графическое построение интерференционной картины для объекта, имеющего вид гребенки (рис 3.6), где проведены указанные параллельные наклонные плоскости через 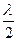, а линии их пересечения спроектированы в плоскость XOY. Анализируя форму интерференционных полос можно определить форму измеряемой поверхности.

Действительно, из треугольника АВС (рис 3.6) следует, что высота h неровности (гребенки)

,

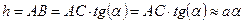(3.8)

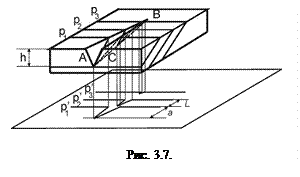где учтена малость угла ; 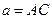- изгиб интерференционной полосы. Известно, что расстояние L между интерференционными полосами в клине связано с углом между его гранями соотношением

.

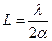(3.9)

Сравнивая (3.8) и (3.9) найдем h – высоту неровности, а вообще говоря, третью координату

Таким образом, получение информации о третьей координаты получается в результате расшифровки интерференционной картины. Проиллюстрируем метод измерения на примере определения глубины царапины АВС на поверхности некоторого объекта (рис 3.7). Согласно вышеизложенного, интерференционные полосы 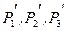получатся как проекции на горизонтальную плоскость (плоскость 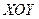согласно рис 3.7) сечений

.

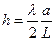(3.10)

параллельными плоскостями 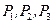поверхности объекта. Измеряя отрезки 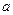- изгиб полосы и 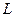- расстояние между полосами по формуле (3.10) определяем глубину .

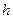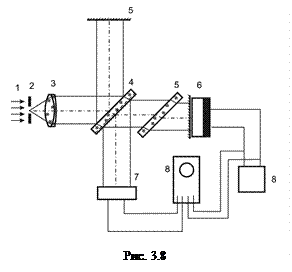Фурье-спектометр. В последние годы интерферометр Майкельсона получил новое применение. Его можно использовать для анализа сложного излучения и получения спектрального разложения. Спектральный прибор, построенный на базе интерферометра Майкельсона, получил название Фурье-спектрометра или спектрометра с частотной модуляцией светового потока. Схема прибора приведена на рис 4.

.

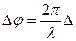(3.11)

Одно из зеркал (6), настроенное на полосы равного наклона, сделано подвижным. Оно может перемещаться параллельно самому себе, будучи закрепленным на пьезокерамическом вибраторе. Разность хода и, соответственно, разность фаз 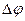интерферирующих пучков будет зависеть от времени следующим образом

Если разность хода будет меняться по линейному закону 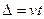, то световой поток на фотоприемнике, а так же ток этого фотоприемника 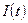, который пропорционален потоку будет функцией времени:

,

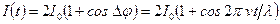(3.12)

где 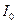-освещенность создаваемая каждым пучком (предполагаемые равными). Таким образом ток фотоприемника оказывается частотно модулированным с частотой 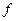, зависящей от длины волны. .

Интерферометр Маха - Цандера. Этот интерферометр, названный в честь из­вестных ученых авиаторов Маха и Цандера, предназначен для изучения поведения воздушных потоков обтекаю­щих как самолеты, так и их отдельные детали. Он, вообще говоря, не отно­сится к типу Май­кельсона, но во многом похож на него. В нем также используется метод деления амплитуд. Схема прибора приведена на рис..3.9. Преобра­зованный в парал­лельный пучок света некой опти­ческой системой (на рисунке не показанной) от источника света 1 попадает на первый делитель 2 и расщепляется на два. Нижний пучок проходит через пустую (эталонную) кювету, и, отразившись от зеркала 3, попадает на второй " делитель" 2, который конст­руктивно полностью эквивалентен первому. Этот элемент выполняет функцию объединения нижнего и верхнего пучка, который, в свою очередь прошел кювету с исследуемым объектом, и на поверхности анализа 6 наблюдается картина их интерференции. Благодаря большому расстоянию между кюветами 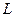, они могут быть достаточно объемными, и в них можно поместить аэродинамические детали и обдувать их потокам воздуха. В силу уравнения Бернулли 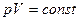, давление воздуха, от которого зависит его показатель преломления, будет функцией скоростей отдельных струй потока и в интерференционной картине эти струи будут визуализированы.

Практически по такой же схеме работает интерферометр Рождественского, но с его помощью решаются другие задачи, в частности и те, для которых используются интерферометры, рассматриваемые ниже.