
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Многолучевая интерференция
|
|
В предыдущих разделах рассматривался случай 2х лучевой интерференции, где было показано, что в случае сложения двух когерентных волн с амплитудами 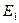 и
и 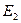 и разностью фаз
и разностью фаз 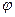 интенсивность суммарного колебания
интенсивность суммарного колебания 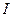 была равна
была равна
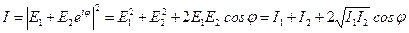 , ,
| (15.1) |
где 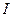 - интенсивность. Так как
- интенсивность. Так как 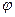 в этом выражении входит только в косинус то график этой интенсивности от
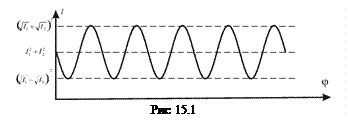
в этом выражении входит только в косинус то график этой интенсивности от 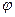 имеет вид (рис)
имеет вид (рис)
Синусоидальный характер такого распределения непригоден для точного определения положения интерференционной картины, так как в нем отсутствую резкие переходы от темного к светлому, так называемые фронты. Это затрудняет или делает невозможным точное совмещение картины с анализирующим устройством: окуляр - микрометром, оптоэлектронным датчиком. Пороговые устройства здесь также малопригодны, из-за того, что пороговое значение такого распределения зависит от величины светового потока формирующего картину. Этот параметр светового излучения зависит от множества факторов и его очень сложно учесть или исключить.
 Отмеченное затруднение может быть преодолено, если в качестве анализируемого распределения использовать интерференционную картину большого числа лучей, т.е. использовать многолучевую интерференцию.
Отмеченное затруднение может быть преодолено, если в качестве анализируемого распределения использовать интерференционную картину большого числа лучей, т.е. использовать многолучевую интерференцию.
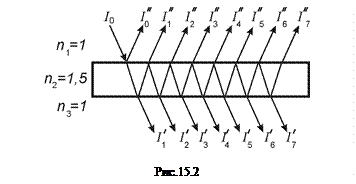 Получим распределение в картине многолучевой интерференции. Подобно двулучевой, практически все случаи формирования этой картины можно свести к интерференции в плоскопараллельной пластине. Рассмотрим этот случай. Пусть имеется плоскопараллельная стеклянная пластинка и на ее грань падает пучок света (рис 15.2). Из рисунка видно, что каждый пучок, кроме первого, отраженный от пластинки дважды проходил через границу раздела воздух стекло и отражался от этих граней
Получим распределение в картине многолучевой интерференции. Подобно двулучевой, практически все случаи формирования этой картины можно свести к интерференции в плоскопараллельной пластине. Рассмотрим этот случай. Пусть имеется плоскопараллельная стеклянная пластинка и на ее грань падает пучок света (рис 15.2). Из рисунка видно, что каждый пучок, кроме первого, отраженный от пластинки дважды проходил через границу раздела воздух стекло и отражался от этих граней 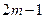 раз, где
раз, где 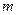 - номер луча. Пучки, вышедшие из пластинки, также дважды проходили через границу раздела воздух стекло, но отражались
- номер луча. Пучки, вышедшие из пластинки, также дважды проходили через границу раздела воздух стекло, но отражались 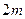 раз. Оценим интенсивности пучков прошедших пластину и отраженных от нее. Ранее было показано, что энергетический френелевский коэффициент отражения
раз. Оценим интенсивности пучков прошедших пластину и отраженных от нее. Ранее было показано, что энергетический френелевский коэффициент отражения 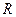 и энергетический коэффициент пропускания
и энергетический коэффициент пропускания 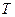 определяются выражениями
определяются выражениями
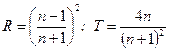 , ,
| (15.2) |
где 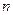 - показатель преломления стекла, которые примем (для простоты) равным 1, 5. Тогда
- показатель преломления стекла, которые примем (для простоты) равным 1, 5. Тогда 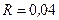 , а
, а 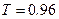 . Считая, что интенсивность падающего пучка
. Считая, что интенсивность падающего пучка 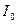 , поместим значения интенсивностей отраженных пучков
, поместим значения интенсивностей отраженных пучков 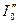 и прошедших
и прошедших 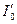 в таблицу 1
в таблицу 1
Табл. 1
Номер луча 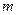
| Отраженные пучки 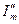
| Прошедшие пучки 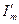
|
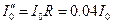
| - | |
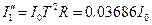
| 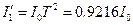
| |
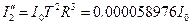
| 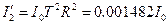
| |
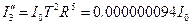
| 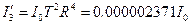
|
Как известно, что контраст интерференционной картины зависит от соотношения интенсивностей интерферирующих пучков - он максимален при равенстве этих интенсивностей, а при увеличении их отношения – падает. Из таблицы следует, что интерференционная картина, которую можно зафиксировать, причем при неплохом контрасте 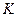 , равном
, равном
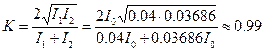 . .
| (15.3) |
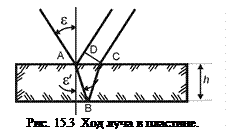 при интерференции пучков лучей
при интерференции пучков лучей 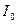 и
и 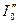 при отражении от стеклянной пластинки. Именно такой контрастом обладают интерференционные картины на тонких пленках, при интерференции в клине и т.п. Однако интенсивность всех остальных пучков, по отношению к падающему, а также по отношению друг к другу настолько мала, что их взаимная интерференция будет практически не заметна. Заметим, что интерференция
при отражении от стеклянной пластинки. Именно такой контрастом обладают интерференционные картины на тонких пленках, при интерференции в клине и т.п. Однако интенсивность всех остальных пучков, по отношению к падающему, а также по отношению друг к другу настолько мала, что их взаимная интерференция будет практически не заметна. Заметим, что интерференция 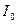 и
и 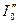 наблюдается из-за того, что их интенсивности относятся как
наблюдается из-за того, что их интенсивности относятся как 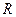 , интенсивности всех же остальных пучков относятся как
, интенсивности всех же остальных пучков относятся как  .
.
Очевидно, для того, чтобы заставить интерферировать большее число лучей, необходимо увеличить коэффициент отражения 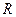 . Этого можно достичь, например, нанося на поверхности отражающие покрытия. Так как определяется интерференционная картина, то необходимо учитывать набег фазы для каждого луча. Разность фаз
. Этого можно достичь, например, нанося на поверхности отражающие покрытия. Так как определяется интерференционная картина, то необходимо учитывать набег фазы для каждого луча. Разность фаз 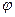 между соседними лучами, которая при этом зависит от угла падения
между соседними лучами, которая при этом зависит от угла падения 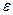 , будет (рис 15.3)
, будет (рис 15.3)
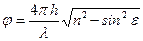 , ,
| (15.4) |
где  - показатель преломления материала пластинки и ее толщина, соответственно,
- показатель преломления материала пластинки и ее толщина, соответственно, 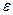 - угол падения,
- угол падения, 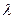 - длина волны излучения.
- длина волны излучения.
Тогда в выражениях в таблице.1 следует вместо интенсивностей 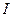 поместить амплитуды
поместить амплитуды 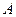 , которые необходимо помножить на соответствующие комплексные амплитуды, учитывающие фазы
, которые необходимо помножить на соответствующие комплексные амплитуды, учитывающие фазы 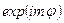 , где
, где 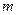 - номер пучка. В этом случае таблица1 будет выглядеть следующим образом. При этом надо учесть то, что энергетические коэффициенты отражения
- номер пучка. В этом случае таблица1 будет выглядеть следующим образом. При этом надо учесть то, что энергетические коэффициенты отражения 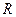 и
и 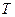 пропускания надо заменить на амплитудные
пропускания надо заменить на амплитудные 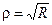 и
и  , которые связаны соотношениями
, которые связаны соотношениями
Табл. 2
Номер луча 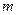
| Отраженные пучки 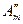
| Прошедшие пучки 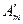
|
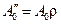
| - | |
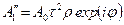
| 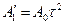
| |
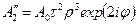
| 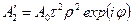
| |
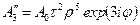
| 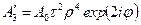
|
В этой таблице для прошедших лучей фаза отсчитывается от первого прошедшего пучка 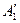 .
.
Рассчитаем суммарную амплитуду прошедших пучков, т.е. их интерференцию, которая, очевидно, будет многолучевой.
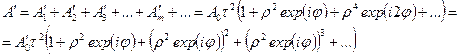
| (15.5) |
Полученное выражение представляет собой бесконечно убывающую геометрическую прогрессию со знаменателем 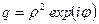 , т.к.
, т.к. 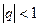 из-за того, что
из-за того, что 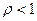 .Суммируя прогрессию и учитывая, что
.Суммируя прогрессию и учитывая, что 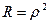 и
и 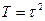 (15.4) получим
(15.4) получим
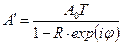 . .
| (15.6) |
Откуда находим интенсивность суммарного пучка как 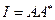
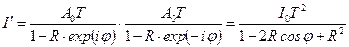 , ,
| (15.7) |
где при выводе была использована формула Эйлера. Тогда коэффициент пропускания всей пластины 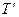 будет
будет
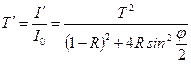 . .
| (15.8) |
Здесь была использована известная тригонометрическая формула  . Полученное выражение называется формулой Эйри. Максимум получаемой интерференционной картины
. Полученное выражение называется формулой Эйри. Максимум получаемой интерференционной картины 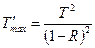 будет при
будет при 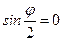 , а минимум
, а минимум 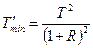 при
при 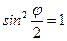 . Отсюда контраст получаемой интерференционной картины
. Отсюда контраст получаемой интерференционной картины 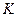 при освещении пластины плоским пучком с равномерным распределением амплитуды будет
при освещении пластины плоским пучком с равномерным распределением амплитуды будет
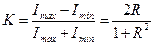 . .
| (15.9) |
Максимум контраста 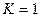 достигается при
достигается при 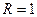 . Вид распределения освещенности при многолучевой интерференции показан на рис 15.4.
. Вид распределения освещенности при многолучевой интерференции показан на рис 15.4.
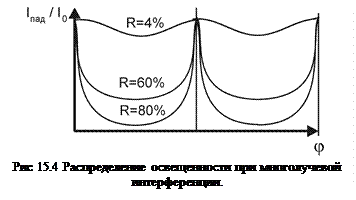 Из вида распределения на графике становится ясно, что предположение о том, что при многолучевой интерференции полосы становятся с более крутыми фронтами и их положение может быть определено с более высокой точностью.
Из вида распределения на графике становится ясно, что предположение о том, что при многолучевой интерференции полосы становятся с более крутыми фронтами и их положение может быть определено с более высокой точностью.
Пластинка Луммера-Герке. Одним из примеров применения многолучевой интерференции является использования ее в спектральном устройстве, называемом пластинкой Луммера-Герке. Эта пластинка сделана из очень однородного материала, а параллельность граней выполнена с высокой точностью (рис.15.5).
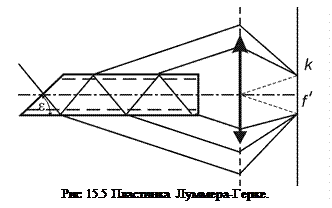 Конец пластинки срезан таким образом, чтобы обеспечить почти нормальное падение конуса лучей, исходящих из источника, а их направление подобрано так, чтобы на границе стекло – воздух было бы почти полное внутреннее отражение, т.е. так, что бы часть лучей конуса выходила из пластинки. А другая часть возвращалась обратно. При этом интенсивность последовательных лучей мало отличаются друг от друга м контраст интерференционной пластинки получается очень высоким. Интерференционная картина представляет ряд очень узких полос разного цвета на темном фоне, т.е. этот прибор позволяет получать спектры с очень высоким разрешением. Расчет показывает, что если пластинка имеет параметры: толщина пластинки
Конец пластинки срезан таким образом, чтобы обеспечить почти нормальное падение конуса лучей, исходящих из источника, а их направление подобрано так, чтобы на границе стекло – воздух было бы почти полное внутреннее отражение, т.е. так, что бы часть лучей конуса выходила из пластинки. А другая часть возвращалась обратно. При этом интенсивность последовательных лучей мало отличаются друг от друга м контраст интерференционной пластинки получается очень высоким. Интерференционная картина представляет ряд очень узких полос разного цвета на темном фоне, т.е. этот прибор позволяет получать спектры с очень высоким разрешением. Расчет показывает, что если пластинка имеет параметры: толщина пластинки 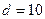 мм, длина
мм, длина 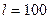 мм, показатель преломления
мм, показатель преломления 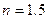 , угол
, угол 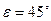 , то разрешающая способность ее
, то разрешающая способность ее 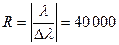 .
.
Интерферометр Фабри-Перо. Это устройство представляет собой две стеклянных пластинки с покрытием, обладающим очень высоким показателем отражения и расположенных параллельно друг друга. Он используется как спектральный прибор и как резонатор лазера.