
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчет деформации ползучести
|
|
При анализе и обобщении экспериментальных данных, полученных при изучении деформации и ползучести, можно использовать различные полуэмпирические уравнения[8], и по величине скорости ползучести 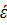 вычислять деформации за заданный интервал времени. Чаще используются έ =S
вычислять деформации за заданный интервал времени. Чаще используются έ =S 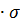 nexp(-Q/RT) (1.1) и έ =S
nexp(-Q/RT) (1.1) и έ =S  exp(
exp(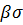 )exp(-Q/RT) (1.2)
)exp(-Q/RT) (1.2)
соответственно для низких и высоких напряжений. Параметры n, Q и Sуравнения, полученные для композиции 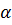 -Al2O3-Н3РО4 при нагрузках 0, 1-0, 8 МПа, представлены в табл. 2. Применение полученных уравнений для указанных в таблице интервалов температур и нагрузках менее 0, 8 МПа позволило рассчитать величины ползучести, отличающихся от экспериментальных на порядок величины. Кроме того, величины параметров уравнения, вычисленные по результатам различных испытаний, имели относительный разброс значений до
-Al2O3-Н3РО4 при нагрузках 0, 1-0, 8 МПа, представлены в табл. 2. Применение полученных уравнений для указанных в таблице интервалов температур и нагрузках менее 0, 8 МПа позволило рассчитать величины ползучести, отличающихся от экспериментальных на порядок величины. Кроме того, величины параметров уравнения, вычисленные по результатам различных испытаний, имели относительный разброс значений до 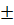 25%.
25%.
Таблица 2.
Значения параметров n, Q и S уравнения ползучести для композиции 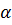 -Al2O3-33мас.%Н3РО4
-Al2O3-33мас.%Н3РО4
| Параметр | В интервале температур 800-1100 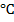
| В интервале температур 1300-1550 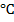
|
| N | 1, 5 | 0, 7 |
| Q, кДж/моль | 100-300 | 160-220 |
S, с-1 (Н  мм-2)-n мм-2)-n
| 8, 36  103 103
| 1, 6  103 103
|
В связи с этим были проведены испытания деформаций в установившемся режиме при Т= 1300, 1400, 1500, 1550 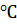 и нагрузках 0, 2 и 0, 4 МПа. Исследуемые образцы имели состав, обладающий max прочностью при Т=1400
и нагрузках 0, 2 и 0, 4 МПа. Исследуемые образцы имели состав, обладающий max прочностью при Т=1400 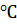 и minдеформацией в неустановившийся период ползучести: э/к №125 – 35%, э/к №20 – 40%, тонкомолотый
и minдеформацией в неустановившийся период ползучести: э/к №125 – 35%, э/к №20 – 40%, тонкомолотый 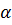 -Al2O3-25%, 85%-наяH3PO4 – 20% сверх 100%. Исходные образцы были термообработаны при 300
-Al2O3-25%, 85%-наяH3PO4 – 20% сверх 100%. Исходные образцы были термообработаны при 300 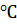 .
.
Обработку полученных результатов проводили по методу обобщенных диаграмм деформации[2, 36], используя уравнение:
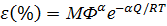 (1.3)
(1.3)
В данном случае: 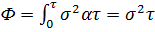 (1.4)
(1.4)
ln 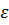 =lnM+
=lnM+ 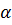 lnФ-α Q/RT=α lnФ-α Q/RT+lnM
lnФ-α Q/RT=α lnФ-α Q/RT+lnM
Используя (1.4) получаем ln 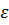 =
= 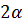 ln
ln 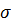 +α ln
+α ln 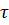 +lnM-α Q/RT
+lnM-α Q/RT
Вводим обозначение: N=lnM-α Q/RT (1.5)
Тогда: N=ln 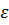 -2α ln
-2α ln 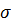 -α ln
-α ln 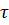 (1.6)
(1.6)
Экспериментально получено:
При Т=1300 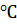 :
:
σ 1=0, 2 МПа 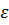 11=0, 4% за τ =16ч Ф11=6, 4
11=0, 4% за τ =16ч Ф11=6, 4  1011Па2
1011Па2  с
с
σ 2=0, 4МПа 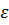 12=0, 5% за τ =16ч Ф12=25, 6
12=0, 5% за τ =16ч Ф12=25, 6  1011Па2
1011Па2  с
с
При Т=1500 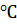 :
:
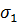 =0, 2 МПа
=0, 2 МПа 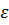 21=0, 54% за τ =16ч Ф21=6, 4
21=0, 54% за τ =16ч Ф21=6, 4  1011Па2
1011Па2  с
с
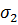 =0, 4 МПа
=0, 4 МПа 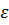 22=0, 64% за τ =16ч Ф22=25, 6
22=0, 64% за τ =16ч Ф22=25, 6  1011Па2
1011Па2  с
с
α 1300=(ln 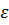 11/
11/ 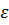 12)/(lnФ11/lnФ12)=0.16
12)/(lnФ11/lnФ12)=0.16
α 1500=(ln 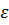 21/ln
21/ln 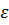 22)/(lnФ21/lnФ22)=0, 12. α ср.=0, 14
22)/(lnФ21/lnФ22)=0, 12. α ср.=0, 14
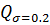 =
= 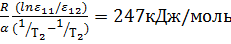
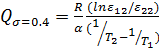 =206 кДж/моль
=206 кДж/моль
Q=(226 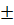 20)кДж/моль
20)кДж/моль
Подставляя в (1.5) вычисленное значение Q, α, а также экспериментальные значения 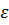 (в%) и заданное значение τ =16ч, находим:
(в%) и заданное значение τ =16ч, находим:
N1300(σ =0.2)=-0.86; N1300(σ =0.4)=-0.82; N’1300=-0.84
N1500(σ =0.2)=-0.56; N1500(σ =0.4)=-0.58; N’1300=-0.57
Тогда, ln 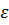 1300=0.28lnσ +0.14lnτ -0.84 (1.7)
1300=0.28lnσ +0.14lnτ -0.84 (1.7)
ln 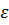 0500=0.28lnσ +0.14lnτ -0.57 (1.8)
0500=0.28lnσ +0.14lnτ -0.57 (1.8)
В этих усл-ях σ выражается в МПа, τ – в часах, пределы изменения σ от 0, 1 до 0, 6 МПа, 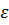 - деформация сжатия в %.
- деформация сжатия в %.
По формулам (1.7) и (1.8) сделан расчет времени деформации (ч) композиции на 1% деформации под нагрузками 0, 1 и 0, 6 МПа при Т=1300 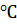 и Т=1500
и Т=1500 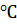 результаты которого приведены в табл. 3.
результаты которого приведены в табл. 3.
Таблица 3.
Время деформации на 1% композиции 35%Э/к№125-40%Э/л№20-25%α -Al2O3-20%(сверх 100) Н3РО4
| Время деформации | Время (ч) на 1% деформации под воздействием нагрузки и температуры | |||
| 0, 1 МПа | 0, 6 МПа | |||
1300 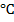
| 1500 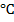
| 1300 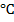
| 1500 
| |
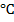 , ч , ч
|
Следует отметить, что полученные уравнения вида ln 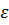 1300=0.28lnσ +0.14lnτ -0.84 и ln
1300=0.28lnσ +0.14lnτ -0.84 и ln 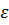 0500=0.28lnσ +0.14lnτ -0.57 позволяют рассчитать время деформации КМ под воздействием нагрузки при различных температурах, и тем самым оценить длительность службы КМ.
0500=0.28lnσ +0.14lnτ -0.57 позволяют рассчитать время деформации КМ под воздействием нагрузки при различных температурах, и тем самым оценить длительность службы КМ.