
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Модели образования и роста зародышей
|
|
Остановимся более детально на следующих случаях и соответствующих теориях:
1. Случайное зародышеобразование в объеме твердого реагента.
Обозначим α f фиктивную степень превращения, не учитывающую поглощение потенциальных центров другими зародышами и перекрывание зародышей; α – истинная степень превращения вещества.
Поскольку предполагается, что зародыши возникают в объеме по закону случая, подразумевая под этим, что топохимически эквивалентные элементы твердого реагента имеют одинаковую вероятность прореагировать, можно записать, что в интервале времени dt
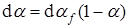 . (39)
. (39)
Это самое простое выражение, удовлетворяющее граничным условиям:
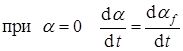 ,
,
т.к. в начале реакции зародышей слишком мало, чтобы их перекрывание или поглощение потенциальных центров играло существенную роль,
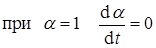 , но
, но 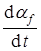 имеет конечное значение.
имеет конечное значение.
Интегрирование уравнения (39) приводит к соотношению, связывающему истинную и фиктивную степени превращения:
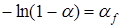 .
.
Ерофеев получил выражение для α в предположении многостадийного зародышеобразования. Его уравнение имеет вид
 , (40)
, (40)
где 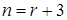 и r имеет смысл числа элементарных стадий при превращении зародыша в активно растущее ядро. В более полном изложении n выражается суммой
и r имеет смысл числа элементарных стадий при превращении зародыша в активно растущее ядро. В более полном изложении n выражается суммой
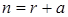 ,
,
где r - число стадий, а а зависит от числа направлений, в которых растут ядра. Так, а = 1, если ядра растут в одном направлении, а = 2 для двух направлений роста ядер, а = 3 для трех направлений.
При малых α, когда α ≈ α f, период ускорения описывается просто степенной функцией.
Константы k и n, входящие в уравнение (40), находят путем графической обработки экспериментальных данных в соответствии с линейной формой уравнения
 .
.
2. Экспоненциальный период ускорения.
Зависимости типа tn наблюдаются для начальных участков (α < 0, 2) кинетических кривых в экзотермических реакциях разложения многих твердых веществ.
Однако очень высокие и плохо воспроизводимые значения показателя n, встречающиеся в некоторых случаях, привели к возникновению концепции зародышеобразования по разветвленному цепному механизму, по которой существующие зародыши в процессе роста инициируют появление новых. Этот механизм может проявляться в различных формах:
1. Образование микроагломератов первичных зародышей, каждый из которых превращается в растущий после “заражения” от соседнего растущего зародыша.
2. Развитие реакции по границам блоков кристаллической структуры (линейные зародыши).
3. Возникновение структурных напряжений, приводящих к увеличению плотности дислокаций и даже к растрескиванию исходной твердой матрицы, что в значительной мере облегчает появление зародышей.
4. Интенсивная диффузия атомов продукта вглубь реагента, опережающая продвижение реакционной поверхности раздела.
Точная форма закона зародышеобразования в данном случае не имеет большого значения, и без большой ошибки можно использовать линейный закон (зародышеобразование с постоянной скоростью). Индуцирование новых зародышей будем характеризовать константой разветвления k 1, не зависящей от α и определяемой как число новых зародышей, которые может инициировать зародыш-предшественник в процессе своего роста. При этих предположениях скорость зародышеобразования запишется в виде
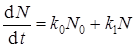 , (41)
, (41)
где k 0 – константа скорости активации исходных центров.
После интегрирования получим
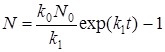 . (42)
. (42)
Подстановка (42) в (41) приводит к явному выражению для скорости зародышеобразования:
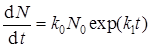 .
.
Гарнер и Хейлз предполагали, что зародыши нитевидные и растут с постоянной скоростью. Чтобы объяснить период спада в этих реакциях, Праут и Томпкинс предположили, что цепи, встречаясь в объеме реагента друг с другом, рвутся, и поэтому прекращается их дальнейший рост. Учесть такой эффект можно путем введения константы k 2, учитывающей вероятность обрыва и зависящей от α.
Выражение (41) для скорости зародышеобразования с учетом скорости обрыва цепей преобразуется к виду
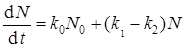 .
.
Обычно второй член этого выражения значительно превосходит первый, поэтому можно записать
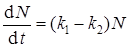 . (43)
. (43)
Поскольку общая теория, позволяющая получить зависимость k 2 от α отсутствует, Праут и Томпкинс провели полуэмпирическое рассмотрение, основанное на особенностях экспериментальной сигмоидной кривой (рис. 28) и на следующих предположениях:
1. Как и в теории Гарнера и Хейлза, константа k 1 считается независящей от α, что вполне приемлемо при рассмотрении модели микроскоплений первичных зародышей, но менее очевидно в тех случаях, когда процесс ветвления обусловлен структурными напряжениями или растрескиванием.
2. В самом начале реакции, когда число зародышей мало, вероятность встречи цепей считается пренебрежимо малой, т.е. k 2 → 0 при α → 0 (условие 1).
3. Полная скорость реакции пропорциональна числу зародышей, существующих в рассматриваемый момент времени t:
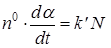 , (44)
, (44)
где n 0 – число молей лимитирующего реагента.
4. Точка перегиба экспериментальной сигмоидной кривой соответствует значению α i = ½. Наиболее распространенным примером реакции, отвечающей этому требованию, является термическое разложение перманганата калия. Именно для объяснения особенностей кинетики этой реакции Праут и Томпкинс создали свою теорию. Симметрия кривой разложения α (t) означает существование периода скрытого разложения, приводящего к формированию первичных зародышей уже в индукционном периоде.
В точке перегиба i скорость dα /dt имеет максимум, т.е.
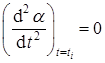 .
.
Из соотношения пропорциональности dα /dt и N следует, что
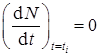 ,
,
откуда k 2 = k 1 при α = α i (условие 2).
Чтобы удовлетворить одновременно условиям 1 и 2, достаточно положить
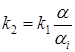 .
.
Исключая из уравнений (43) и (44) время и k 2, находим
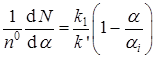 .
.
Интегрирование этого выражения дает зависимость N(α), которую достаточно подставить в уравнение (44), чтобы получить уравнение для полной скорости реакции:
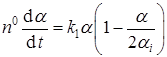 .
.
Интегрирование этого выражения в пределах от (α 0, t0) до (α, t) приводит к уравнению Праута-Томпкинса, которое при α i = ½ имеет вид
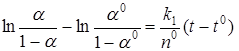 . (45)
. (45)
Это уравнение удовлетворительно описывает термическое разложение многих солей, в особенности перманганатов, свежеприготовленного оксалата свинца, формиата никеля в области 0, 1 < α < 0, 9. Оно применимо также к некоторым другим типам реакций, в частности, для описания сульфидирования сероводородом хлоридов Ni, Co, Cu и т.д.
Однако это уравнение следует рассматривать как приближенное, если хотя бы некоторые из сформулированных выше предположений не реализуются. Кроме того, необходимо заметить, что идея разветвленного цепного механизма зародышеобразования вовсе не обязательна для получения зависимости α (t) вида (45). Иногда при анализе экспериментальных данных используют такую форму уравнения Праута-Томпкинса:
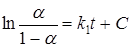 .
.
При настоящем уровне развития кинетики топохимических реакций часто бывает трудно решить, какой модели и, следовательно, какому уравнению следует отдать предпочтение.