Параметры идеальных газовых смесей

Для идеальных газов давление р газовой смеси равняется сумме парциальных давлений р_i, всех компонентов (закон Дальтона):

. (1.1)

Под парциальным давлением понимается давление, которое имел бы данный компонент, если бы он один занимал объем V смеси при температуре смеси Т.

На основании уравнения состояния

, (1.2)

где С_i - мольная концентрация i -го компонента; R_m - универсальная газовая постоянная.

Подставив p_i в (1.1) и учитывая, что - суммарная концентрация, получим, что смесь газов также подчиняется уравнению состояния

, (1.3)

где v_m - молярный объем. Задание газовых смесей путем относительной молярной концентрации

. (1.4)

Подставив сюда С_i и С из (1.2) и (1.3), получим

. (1.4 ')

Обозначим через V_i объем компонента i при давлении р и температуре Т. Тогда

,

Учитывая (1.3), получим

,

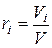где r_i – относительная объемная доля i-го компонента.

Состав смеси можно характеризовать также массовыми долями разных компонентов:

,

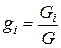где G - общая масса смеси в объеме V, G_i - масса компонента в том же объеме.

Установим связь между g_i и r_i. Для идеального газа

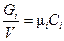(1.5)

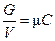, (1.5 ')

где m _i - молекулярный вес компонента i, m - средний или кажущийся молекулярный вес смеси.

Суммируя уравнение (1.5) по i и сравнивая с (1.5 '), находим m:

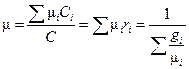, (1.6)

а, поделив уравнение (1.5) на (1.5 '), получим искомую связь между g_i, и r_i:

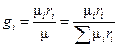, или . (1.7)

Для «весовой» концентрации, т. е. плотности ρ =С/m, уравнение состояния (1.3) принимает вид

,

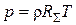где - газовая постоянная смеси.