Характеристика состава горючей смеси

Важной характеристикой горючей смеси является коэффициент избытка окислителя (воздуха)

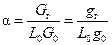, (1.8)

где L ₀ - стехиометрический коэффициент, т. е. количество окислителя, требующегося для стехиометрического сжигания 1кг горючего; G_г, G₀ - соответственно веса горючего и окислителя в смеси.

«Богатая смесь», если a< 1, «бедная смесь», если a> 1. Если a=1, то смесь стехиометрическая.

Пример. Пусть состав горючего характеризуется величинами g_Cг, g_Hг, g_Ог и окислителя g_Co, g_Но, g_Оo. Стехиометрические реакции горения:

,

.

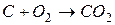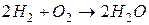Если моли выразить в килограммах, то, например, для сгорания 4кг Н ₂ требуется 32кг О ₂, или на 1кг Н ₂ нужно 8кг О ₂. Тогда на 1кг горючего кислорода (кг) нужно:

.

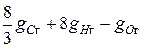В 1кг окислителя свободного кислорода содержится

,

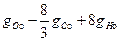где g_Сo и g_Но - весовое содержание С и Н в 1кг окислителя, на сжигание которых необходимо затратить некоторое количество О ₂. Следовательно,

. (1.9)

Если окислитель - воздух, то g_{H o}=0, g_Co=0 и g_Оo=0, 232, откуда

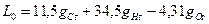. (1.10)

Например, для керосина (состав: g_C=0, 86 и g_H=0, 14) в воздухе L ₀=14, 75кг воздуха на 1кг керосина.

1.4. Классификация и общие свойства углеводородов

Нефть и природный газ являются смесью различных углеводородов. Углеводородные горючие классифицируются по гомологическим рядам. Наиболее стабильными являются углеводороды парафинового или метанового ряда. Состав парафинов характеризуется формулой C_nH_2n+2. Структурная формула нормальных парафинов

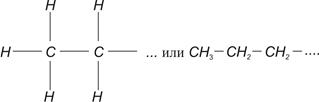
При n> 3 существуют изомеры с разветвленной цепью. Примером могут служить н-бутан и изобутан, структурные формулы которых соответственно имеют вид

СН₃ — СН₂ — СН₂ — СН₃ и СН₃ — СН — СН₃.

ï

СН₃

При малых n парафины являются газами при нормальных условиях, например метан СН₄, бутан С₄Н₁₀. При 5< n< 16 парафины являются жидкостями, например октан С₈Н₁₈. При n> 16 парафины находятся в твердом состоянии.

Нафтеновый ряд (или циклопарафины) имеют состав С_nН_2n. Циклопарафины получаются из парафинов путем удаления из цепи крайних атомов Н и замыкания цепи в кольцо, как это можно видеть на примере циклопропана С₃Н₆:

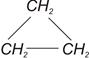
Циклопарафины — это относительно прочные соединения, не реагирующие ни с серной кислотой, ни со щелочами.

Ароматический, или бензольный, ряд имеет состав С_пН_2n-6. Это непредельные углеводороды циклического строения. Начальным членом ряда является бензол С₆Н₆:

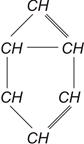
В сложных ароматиках один или несколько атомов Н в кольце замещаются алкильной группой СН₃. Примером может служить толуол С₇Н₈. Ароматические углеводороды характеризуются высокой стойкостью против детонации в двигателях.

Этиленовый, или олефиновый, ряд относится к непредельным углеводородам с двойными связями состава С_пН_2n. Представителями этого ряда являются: этилен СН₂==СН₂, пропилен СН₃—СН==СН₂ и т.д. Олефины легко присоединяют водород и превращаются в предельные углеводороды. Поэтому при длительном хранении в обычных условиях они неустойчивы.

Фракционный состав продуктов переработки нефти характеризуется кривой разгонки, которая представляет собой зависимость между испарившейся долей горючего и температурой смеси.

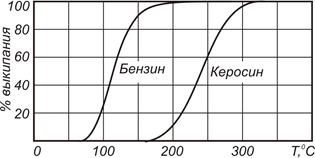
Рис. 1.1. Кривые разгонки для легкого бензина

и тракторного керосина

На рис. 1.1 изображены кривые разгонки для бензина и для тракторного керосина. Видно, что 98% бензина испаряется при температуре 180°С. Для керосина это наступает только при 300°С. При температуре больше 350°С почти все высокомолекулярные углеводороды разлагаются (крекинг) с образованием более легких молекул.

При сгорании молекулы углеводорода конечными продуктами получаются углекислота и вода. Чем сложнее молекула, тем больше энергии заключено во внутренних связях и тем меньше тепловой энергии выделяется при сгорании одной молекулы в расчете на единицу веса. Например, для парафинового ряда теплота сгорания метана СН₄ составляет 212, 8ккал/моль, а гексана С₆Н₁₄ составляет 1002, 4. Молекулярный вес метана и гексана соответственно равняется 16 и 86, и, следовательно, теплотворные способности (высшие) получаются соответственно 13200 и 11650ккал/кг.

Известно, что в гомологических рядах энергетические интервалы между членами ряда примерно постоянны. В парафиновом ряду присоединение каждой новой метиленовой группы СН₂ вызывает увеличение теплоты реакции на 157, 5ккал/моль. Таким образом, теплота реакции углеводородов парафинового ряда С_пН_2n+2 может быть вычислена [11] по формуле

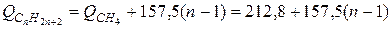ккал/моль,

что дает на единицу веса

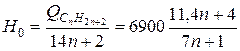ккал/кг.

В [11] приводится также обобщенная формула для расчета высшей теплотворной способности углеводородов типа С_пН_2n+2а:

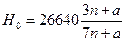ккал/кг.

2. Некоторые сведения из химической кинетики

2.1. Скорость простых химических реакций

Скорость реакции выражается формулой

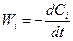, (2.1)

где C_i - концентрация одного из исходных компонентов, участвующих в реакции. В зависимости от размерности C_i меняется и размерность W_i. Знак «минус» использован для того, чтобы W_i была положительна, поскольку в процессе реакции C_i уменьшается. Для продуктов реакции C_j. В этом случае

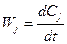, (2.2)

Обоснование закона (действующих масс) в том, что реакция осуществляется только при взаимных столкновениях молекул, а частота столкновений пропорциональна концентрациям.

Скорость прямой реакции:

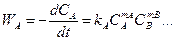, (2.3)

где коэффициент k _A, зависящий от температуры и вида реакции, называется константой скорости реакции. Размерность k _A зависит от m_A, m_B и от размерности C и t.

Скорость обратной реакции:

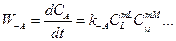. (2.4)

где индекс -А показывает, что данная величина относится к обратной реакции.

В смеси исходных веществ и продуктов реакции наблюдаются два противоположных процесса: один сопровождается исчезновением молекул А, а другой, наоборот, их появлением. Суммарное уменьшение концентрации С_A будет происходить со скоростью

W=W_A - W_-A.

Рано или поздно скорости W_A и W_-A сравняются, так что суммарная скорость станет равной нулю. Наступит состояние химического равновесия. В этом случае

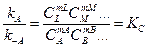, (2.5)

где К _C - константа равновесия. Зная К _C и константу скорости какой-либо реакции, можно найти константу скорости обратной реакции:

.

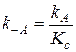Если скорость реакции пропорциональна первой степени концентрации только одного из компонентов, например А, а от концентрации остальных компонентов не зависит, то кинетическое уравнение (первого порядка) имеет вид

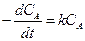. (2.6)

Кинетическое уравнение второго порядка:

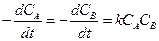. (2.7)

Этим уравнением описываются все бимолекулярные реакции, т.е. такие, в которых участвуют две молекулы и реакция происходит при их соударении (m_A=m_B=1; m_С=...=0). Уравнение второго порядка может быть применено и для сложных реакций, если определяющая стадия этой реакции идет по бимолекулярному механизму.

Для реакций третьего порядка уравнение

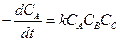. (2.8)

Химическая реакция здесь происходит при одновременном соударении трех молекул (тримолекулярная реакция).

Если пренебречь скоростью обратной реакции, то уравнение (2.8) - дифференциальное. Обозначив начальную концентрацию реагирующего вещества через а, после интегрирования при k=const (т. е. для изотермической реакции) получим

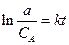. (2.9)

Характеристическое время t _е - время, в течение которого начальная концентрация а уменьшается в е раз («время релаксации»). Время полураспада t_1/2 - время, в течение которого а уменьшается в два раза.

Из (2.9) получим

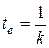и .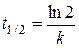

Значения t _е и t_1/2 не зависят от начальной концентрации а. Измеряя в эксперименте эти времена, можно однозначно определить константу скорости реакции первого порядка.

Аналогично для реакции второго порядка А+В при начальных концентрациях а и b получим после интегрирования (2.8)

при k=const

,

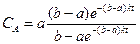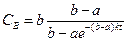
откуда

.

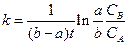В частном случае, когда C_А= C _В= C и а = b, имеем

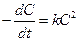и .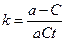

Отсюда время полураспада 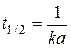, т. е. зависит от начальной концентрации.

Измерив время полураспада для смеси исходных веществ, взятых в одинаковых концентрациях а ₁, и затем повторив опыт для другой концентрации а₂, можно сравнить времена t ₁ и t ₂. Если t ₁» t ₂, то реакция первого порядка. Если t ₁/ t ₂» а ₂/ а ₁, то реакция второго порядка и т. д. Для реакций любого порядка m можно показать, что при одинаковых начальных концентрациях

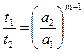. (2.10)