Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Интегральное кинетическое уравнение
|
|
На практике чаще всего интересует не само значение скорости химической реакции, а то, сколько вещества израсходовано или образовалось к определенному моменту времени после начала реакции.
Рассмотрим эту задачу на примере реакции первого порядка
А ® продукты.
Скорость такой реакции выражается следующим уравнением:
 .
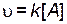| (2.6) |
В дифференциальном виде
 .
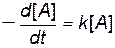| (2.7) |
Перепишем это уравнение в следующем виде:
,
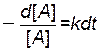и возьмем определенный интеграл от обеих частей уравнения от исходного состояния ([ A ]0, t 0 = 0) до текущего момента ([ A ]t, t):
.
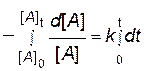Решение этого уравнения приводит к следующей зависимости:
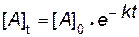
| (2.8) |
или
 .
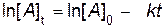| (2.9) |
Соотношения (2.8) и (2.9) являются интегральными кинетическими уравнениями реакции первого порядка.
Зная исходную концентрацию вещества [ A ]0 и константу скорости реакции k, можно рассчитать концентрацию [ A ]t через любое время t после начала реакции.
Если же известны исходная концентрация [ A ]0 и концентрация реагирующего вещества [ A ]t через какое-то время t после начала реакции, то можно рассчитать константу скорости этой реакции
 .
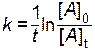| (2.10) |
Часто для характеристики скорости реакции пользуются временем полупревращения t 1/2 (для реакции первого порядка чаще говорят «период полураспада»). t 1/2 - это время, за которое прореагирует половина исходного вещества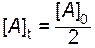 
. Тогда, исходя из уравнения (2.10), получим следующие зависимости:
 ;
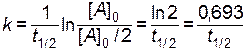| (2.11) |
  .
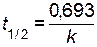| (2.12) |