
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Примеры решения типовых задач
|
|
Пример 1. Как изменится начальная скорость простой реакции образования NOСl2
2NO(г)+ Cl2(г) = 2NOCl2(г),
если уменьшить объем газовой смеси в 2 раза?
Решение. Скорость данной реакции равна
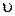 = k [NO]2[Cl2 ].
= k [NO]2[Cl2 ].
Если обозначить концентрации NO и Cl2 до изменения объема, соответственно, через a и b, тогда 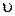 = k ∙ a 2∙ b.
= k ∙ a 2∙ b.
В результате уменьшения объема в 2 раза концентрации NO и Cl2 увеличиваются в 2 раза, и скорость реакции станет равна
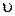 * = k (2 a)2 ∙ 2 b = 8 k ∙ a 2∙ b = 8
* = k (2 a)2 ∙ 2 b = 8 k ∙ a 2∙ b = 8 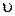 .
.
Тогда 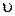 */
*/ 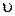 = 8. Таким образом, скорость реакции увеличится в 8 раз.
= 8. Таким образом, скорость реакции увеличится в 8 раз.
Пример 2. Скорость разложениявещества А описывается кинетическим уравнением первого порядка. Определить концентрацию вещества А через 100 с после начала реакции, если известно, что начальная концентрация его составляла 0, 01 моль/л, а константа скорости равна 0, 023 с-1.
Решение. Используя интегральное кинетическое уравнение реакции первого порядка (2.9), имеем
ln[ A ]t = ln[ A ]0 – kt;
ln[ A ]t = ln0, 01 – 0, 023 × 100;
ln[ A ]t = – 6, 9; [ A ]t =0, 001 моль/л.
Пример 3. Определить, за какое время израсходуется 90% исходного вещества, если известно, что скорость реакции описывается кинетическим уравнением первого порядка, а константа скорости равна 4, 6 × 10-2 с-1.
Решение. Если вещества А было 100%, израсходовано 90% (конверсия вещества), то к времени t останется 10% вещества. Подставляя эти значения в уравнение (2.9), найдем
ln[ A ]t = ln[ A ]0 – kt,
ln10 = ln100 – 4, 6 × 10-2 × t
t = 50 с.
Пример 4. Известно, что скорость разложения вещества А описывается кинетическим уравнением первого порядка. Определить концентрацию вещества через 100 с после начала реакции, если известно, что исходная концентрация его была 0, 4 моль/л, а время полупревращения 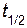 равно 30 с.
равно 30 с.
Решение. Для нахождения константы скорости реакции воспользуемся уравнением (2.12)
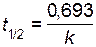 ,
,
откуда
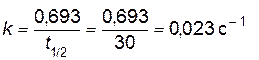 .
.
Тогда концентрация через 100 с после начала реакции
ln[ A ]t = ln[ A ]0 – kt;
ln[ A ]t = ln 0, 4 – 0, 0231.100 = – 0, 916 – 2, 31 = – 3, 226
[ A ]t = е - 3, 226 = 0, 0397 моль/л.
Пример 5. Для некоторой реакции
n А + m В ® продукты,
проводимой при различных исходных концентрациях реагирующих веществ, экспериментально определяли скорость реакции: сначала при различных концентрациях вещества В и фиксированной концентрации вещества А (опыты 1-3), затем при различных начальных концентрациях А и постоянной концентрации В (опыты 4-6). Полученные данные представлены в табл. 1.
Таблица 1
| Величины | Номер опыта | |||||
| [A], моль/л | 1, 3 | 1, 3 | 1, 3 | 0, 1 | 0, 3 | 0, 5 |
| [ B ], моль/л | 0, 2 | 0, 4 | 0, 6 | 1, 3 | 1, 3 | 1, 3 |
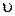 , моль/л× с , моль/л× с
| 0, 0208 | 0, 0832 | 0, 1871 | 0, 0676 | 0, 2028 | 0, 3381 |
Определить вид дифференциального кинетического уравнения и константу скорости реакции.
Решение. Зависимость начальной скорости от концентрации для данной реакции выражается дифференциальным кинетическим уравнением
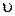 = k [ A ]n [ B ]m.
= k [ A ]n [ B ]m.
Прологарифмируем это выражение
ln 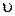 = ln k + n ln[ A ] + m ln[ B ]. = ln k + n ln[ A ] + m ln[ B ].
|
Величины k, n и m для рассматриваемой реакции (при Т = const) являются постоянными и не зависят от концентрации реагентов.
Так как в трех опытах (1-3) концентрация вещества А постоянна (обозначим ее [ A ]0), то в уравнении сумма (ln k + n ln[ A ]0) будет тоже величиной постоянной. Обозначим ее
ln k + n ln[ A ]0 = D1.
Тогда уравнение можно переписать так:
ln 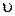 = m ln[ B ] +D1.
= m ln[ B ] +D1.
Зависимость представляет собой в координатах ln[ B ] — ln 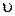 уравнение прямой линии, тангенс угла наклона которой к оси абсцисс равен порядку реакции по веществу В.
уравнение прямой линии, тангенс угла наклона которой к оси абсцисс равен порядку реакции по веществу В.
В табл. 2 представлены значения логарифмов концентраций и скоростей для опытов (1-6).
Таблица 2
| Величины | Номер опыта | |||||
| ln[ A ] | 0, 2624 | 0, 2624 | 0, 2624 | -2, 3026 | -1, 2040 | -0, 6931 |
| ln[ B ] | -1, 6090 | -0, 9163 | -0, 5108 | 0, 2624 | 0, 2624 | 0, 2624 |
ln 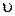
| -3, 8728 | -2, 4865 | -1, 6761 | -2, 6941 | -1, 5955 | -1, 0844 |
По результатам опытов (1-3) построим график зависимости ln 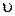 от ln[ B ] (рис. 13) и найдем порядок реакции по веществу B
от ln[ B ] (рис. 13) и найдем порядок реакции по веществу B
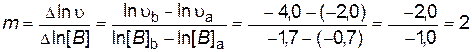 .
.
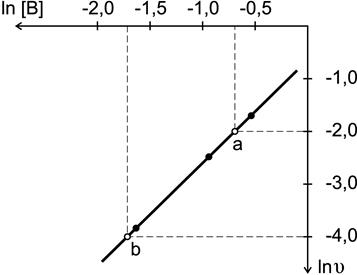
Рис. 13. Определение порядка реакции по веществу В
В последующих опытах (4-6) концентрация вещества B остается постоянной ([ B ]= [ B ]0), поэтому
ln k + m ln[ B ]0 = D 2
ln 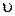 = n ln[ A ] + D 2.
= n ln[ A ] + D 2.
По результатам опытов (4-6) построим график зависимости ln 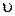 от ln[ А ] (рис. 14) и найдем порядок реакции по веществу А
от ln[ А ] (рис. 14) и найдем порядок реакции по веществу А
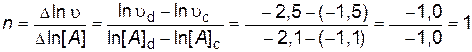 .
.
Рис.14. Определение порядка реакции по веществу А
Таким образом, зависимость скорости от концентрации для исследуемой реакции
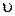 = k [ A ]1 [ B ]2.
= k [ A ]1 [ B ]2.
В этом уравнении порядок реакции по веществу B равен 2, а порядок реакции по веществу A равен 1. Сумма порядков по реагирующим веществам, равная 3, дает общий порядок реакции.
Для определения константы скорости прологарифмируем дифференциальное кинетическое уравнение с учетом полученных порядков реакции по веществам A и B
ln k = ln 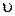 – ln[ А ] – 2ln[ В ].
– ln[ А ] – 2ln[ В ].
Вычислив константу скорости реакции для каждого опыта (в табл. 3 представлены данные для трех опытов), найдем среднее значение константы
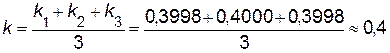 л² · моль-2·с-1.
л² · моль-2·с-1.
Таблица 3
| Величины | Номер опыта | ||
| ln[ A ] | 0, 2624 | 0, 2624 | 0, 2624 |
| ln[ B ] | – 1, 6090 | – 0, 9163 | – 0, 5108 |
ln 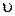
| – 3, 8728 | – 2, 4865 | – 1, 6761 |
| ln k | – 0, 9172 | – 0, 9163 | – 0, 9169 |
| k | 0, 3998 | 0, 4000 | 0, 3998 |
Таким образом, дифференциальное кинетическое уравнение имеет вид
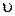 = 0, 4 [ A ][ B ]2.
= 0, 4 [ A ][ B ]2.
Пример 6. Определить энергию активации Еа реакции, для которой при повышении температуры от 22 до 32 °C константа скорости возрастает в 2 раза.
Решение. Запишем уравнение Аррениуса для двух температур в виде
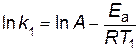 ,
,
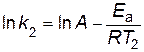 .
.
В результате вычитания первого уравнения из второго, получим
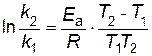 ,
,
следовательно,
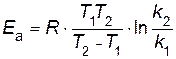 .
.
Отношение k 2 / k 1= 2 по условию. Переводим температуру в Кельвины и подставляем значения в уравнение
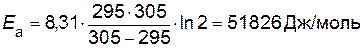 .
.
Пример 7. Энергия активации некоторой реакции при отсутствии катализатора равна 75 кДж/моль, а с катализатором 50 кДж/моль. Во сколько раз возрастет скорость реакции в присутствии катализатора, если реакция протекает при 25°C?
Решение. Обозначим энергию активации реакции без катализатора через  , а с катализатором – через
, а с катализатором – через 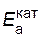 ; соответствующие константы скорости реакции обозначим через
; соответствующие константы скорости реакции обозначим через 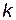 и
и 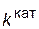 . Предположим, что величина А для данной реакции постоянна и не зависит от присутствия катализатора. Используя уравнение Аррениуса, находим
. Предположим, что величина А для данной реакции постоянна и не зависит от присутствия катализатора. Используя уравнение Аррениуса, находим
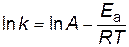 ,
,
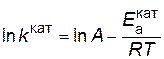 .
.
В результате вычитания первого уравнения из второго
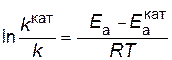 .
.
Подставляя в последнее уравнение данные задачи, выражая энергию активации в Джоулях и учитывая, что Т = 298 К, получим
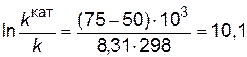
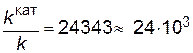 .
.
Таким образом, в присутствии катализатора скорость реакции возрастет в 24 тысячи раз.
Пример 8. Приведенные ниже данные соответствуют температурной зависимости константы скорости реакции, имеющей первый порядок
| Температура T, К | ||||
| Константа k, с-1 | 0, 0017 | 0, 0036 | 0, 0055 | 0, 0125 |
Определите энергию активации и значение предэкспоненциального множителя. Рассчитайте константу скорости при температуре T=303 K.
Решение. Согласно уравнению Аррениуса зависимость константы скорости от температуры имеет вид
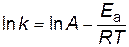 ,
,
поэтому необходимо построить график зависимости 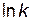 от
от 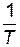 .
.
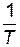
| 0, 00364 | 0, 00353 | 0, 00347 | 0, 00336 |
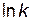
| – 6, 38 | – 5, 63 | – 5, 20 | – 4, 38 |
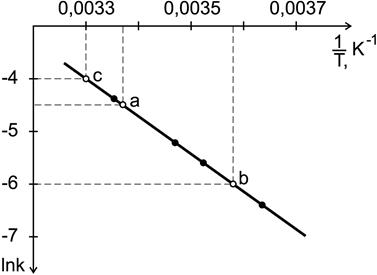
Рис.15. Определение энергии активации
Энергию активации можно определить из тангенса угла наклона прямой (рис. 15)
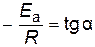 ;
;
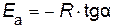 ;
;
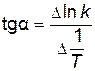 ;
;
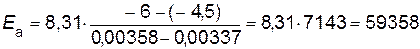 Дж/моль.
Дж/моль.
Определим значения предэкспоненциального множителя. Для произвольной точки на прямой зависимости 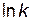 —
— 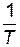 , например, точки а, найдем соответствующие ей значения:
, например, точки а, найдем соответствующие ей значения: 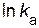 = – 4, 5;
= – 4, 5; 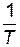 = 0, 00337.
= 0, 00337.
Подставляем значения 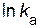 ,
, 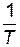 и
и  в уравнение Аррениуса
в уравнение Аррениуса
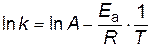 ,
,
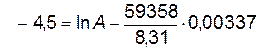 ,
,
откуда
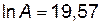 ;
; 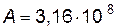 .
.
Подставляя найденные значения энергии активации и предэкспоненциального множителя в уравнение Аррениуса, получим зависимость константы скорости от температуры
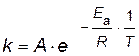 ;
;
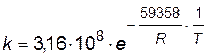 ;
;
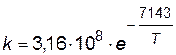 .
.
Найдем значение константы скорости при температуре Т=303К
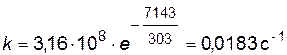
или по уравнению
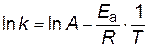 ;
;
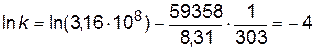 ;
;
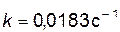 .
.
Можно определить константу скорости и непосредственно из графика (рис.15). Отложив на оси 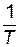 значение
значение 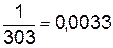 (точка c), находим по графику
(точка c), находим по графику 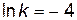 ;
; 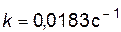 .
.
Пример 9. Константа равновесия реакции А + В «C + D равна единице. Исходные концентрации: [ А ]0 = 0, 01моль / л, [ В ]0 = 0, 03 моль / л. Определить равновесные концентрации всех четырех веществ.
Решение.
1. Пишем уравнение реакции.
2. Для каждого из участников реакции записываем начальные концентрации исходных веществ (в моль/л). Т.к. начальные концентрации продуктов реакции не оговариваются в условии задачи, то принимаем их равными нулю.
3. По уравнению реакции определяем изменение концентраций всех веществ к моменту достижения равновесия. Из уравнения реакции видно, что из каждого моля А и В образуется по одному молю С и D. Принимаем, что в ходе реакции к моменту достижения равновесия прореагировало x моль/л вещества А. Если прореагирует х молей А, то должно прореагировать также х молей В, в то же время должно образоваться по х молей С и D.
5. Определяем равновесные концентрации веществ. При протекании реакции в прямом направлении до состояния равновесия происходит уменьшение концентраций исходных веществ и увеличение концентраций продуктов реакции.
А + В «С + D
Начальное
состояние 0, 01 0, 03 0 0
Число молей
по уравнению 1 1 1 1
Изменение
концентраций x x x x
Равновесное
состояние 0, 01 – x 0, 03 – x x x
6. Пишем выражение закона действующих масс. Подставляем в него найденные значения равновесных концентраций.
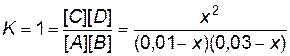 .
.
7. Решаем уравнение. При этом учитываем, что отрицательный корень не имеет физического смысла, и убыль концентрации исходного вещества не может быть больше величины самой концентрации. х = 0, 0075 моль / л.
8. Находим равновесные концентрации.
[ А ] = [ А ]0 – x = 0, 01 – 0, 0075 = 0, 0025 моль / л;
[ B ] = [ B ]0 – x = 0, 03 – 0, 0075 = 0, 0225 моль / л;
[ C ] = x = 0, 0075 моль / л;
[ D ] = x = 0, 0075 моль / л.
Пример 10. В системе А(г) + В(г) «2С(г) равновесные концентрации равны: [ А ] = 0, 018 моль / л, [ В ] = 0, 011 моль / л, [ С ] = 0, 016 моль / л. Найти константу равновесия реакции и исходные концентрации веществ А и В.
Решение. Константа равновесия данной реакции выражается уравнением
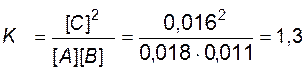 .
.
Для нахождения исходных концентраций веществ А и В учтем, что, согласно уравнению реакции, из 1 моля А и 1 моля В образуется 2 моля С. Поскольку по условию задачи в каждом литре системы образовывалось 0, 016 моля вещества С, то при этом было израсходовано 0, 008 моля вещества А и 0, 008 моля вещества В.
А + В «2 С
Начальное
состояние??
Число молей
по уравнению 1 1 2
Изменение
концентраций 0, 008 0, 008 0, 016
Равновесное
состояние 0, 018 0, 011 0, 016
Таким образом, исходные концентрации равны:
[ А ]0 = 0, 018 + 0, 008 = 0, 026 моль / л;
[ В ]0 = 0, 011 + 0, 008 = 0, 019 моль / л.
Пример 11. Химическое равновесие гомогенной реакции
A + B «2D,
протекающей при T = const, установилось при следующих концентрацияхреагирующих веществ: [ А ] = 0, 4 моль/л; [ В ] = 0, 2 моль/л; [ D ] =0, 4 моль/л. Затем концентрацию вещества B увеличили до 0, 5 моль/л. Рассчитайте новые равновесные концентрации реагирующих веществ.
Решение. Вычислим константу равновесия данной реакции:
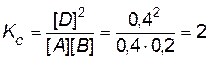 .
.
После добавления вещества B возникло новое состояние системы с концентрациями [А]=0, 4 моль/л; [В] = 0, 5 моль/л; [D] = 0, 4 моль/л.
В соответствии с принципом Ле Шателье при увеличении концентрации [ В ] равновесие сместится в сторону прямой реакции.
Движение системы к новому состоянию равновесия должно сопровождаться увеличением концентрации D и снижением концентрации A и B.
Если концентрация вещества A снизится на x моль/л, то в соответствии с уравнением реакции концентрация вещества B должна уменьшиться на такую же величину и концентрация вещества D –увеличиться на 2 x моль/л. Тогда равновесные концентрации будут равны: [ А ] = 0, 4 – x; [ В ] = 0, 5 – x; [ D ] = 0, 4 + 2 x.
Реакция протекает при постоянной температуре, следовательно, константа равновесия 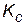 останется прежней, равной 2. Подставляем новые равновесные концентрации реагирующих веществ в выражение константы равновесия:
останется прежней, равной 2. Подставляем новые равновесные концентрации реагирующих веществ в выражение константы равновесия:
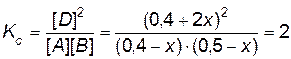 .
.
Откуда x = 0, 07.
А + В «2D
Начальное
равновесное
состояние 0, 4 0, 2 0, 4
Состояние системы
после добавления
вещества B 0, 4 0, 5 0, 4
Число молей
по уравнению 1 1 2
Изменение
концентраций x x 2x
Новое
равновесное
состояние 0, 4 – x 0, 5 – x 0, 4 + 2x
Новые равновесные концентрации:
[ А ] = 0, 4 – x = 0, 4 – 0, 07 = 0, 33 моль/л;
[ В ] = 0, 5 – x = 0, 5 – 0, 07 = 0, 43 моль/л;
[ D ] = 0, 4 + 2 x = 0, 4 + 0, 14 = 0, 54 моль/л.
Если в качестве проверки подставить значения новых равновесных концентраций в выражение константы равновесия, получим
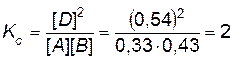 .
.
Пример 12. Эндотермическая реакция разложения пентахлорида фосфора протекает по уравнению
PCl5 (г) «PCl3 (г) + Cl2 (г); DН = +92, 59 кДж.
Как надо изменить: а) температуру; б) давление; в) концентрации реагирующих веществ, чтобы сместить равновесие в сторону прямой реакции – разложения PCl5?
Решение. В соответствии с принципом Ле Шателье, если на систему, находящуюся в состоянии равновесия, оказать внешнее воздействие, то смещение равновесия происходит в сторону той реакции (прямой или обратной), которая ослабляет эффект внешнего воздействия.
1. Смещение равновесия при изменении температуры связано с тепловым эффектом реакции. Так как рассматриваемая реакция эндотермическая (DН > 0), то для смещения равновесия в сторону прямой реакции нужно повысить температуру.
2. Так как в данной реакции разложение PCl5 ведет к увеличению объёма (из одного моля газа образуются два), то для смещения равновесия в сторону прямой реакции надо уменьшить давление.
3. Чтобы сместить равновесие в сторону прямой реакции, необходимо увеличить концентрацию PCl5.