Интерференция волн. Интерференцияволн – это явление устойчивого во времени усиления или ослабления колебаний в разных точках пространства

Интерференция света

Интерференцияволн – это явление устойчивого во времени усиления или ослабления колебаний в разных точках пространства, которое происходит при наложении двух или более волн. Интерференция возможна для волн любой природы. Наиболее интересны проявления интерференции электромагнитных (световых) волн. Интерференция света характеризуется чередованием в пространстве областей повышенной и пониженной интенсивности, которые возникают в результате наложения так называемых когерентных волн.

Интерференция волн

Экспериментально наблюдаемые величины, такие как освещенность поверхности, характеризуются энергией электромагнитных волн. Эта энергия определяется величиной вектора Умова-Пойтинга. Однако из-за очень большой частоты колебаний векторов 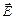и 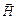в световой волне видимого диапазона невозможно измерить мгновенное значение энергии волны, так как всем приемникам присуща определенная инерционность. Это означает, что любое регистрирующее устройство реагирует на изменение физических величин, время изменения которых не меньше определенной величины. Это время называют временем разрешения приемника. У человеческого глаза оно ~ 0, 1 с, у фотоматериалов 10 ^{– 2} ¸ 10 ^{– 4} с. Существуют и другие приемники, у которых время разрешения достигает 10 ^{– 8} ¸ 10 ^{– 10} с. Однако, даже такие времена велики по сравнению с периодом оптических колебаний ~ 10 ^{– 15} с.

Рассмотрим две электромагнитные волны одинаковой частоты w₁ = w₂ = w, которые, накладываясь друг на друга, возбуждают в некоторой точке пространства два колебания одинакового направления. Поскольку электрическая и магнитная составляющие электромагнитных волн колеблются в одинаковой фазе, достаточно рассмотреть только одну из них. Как уже отмечалось в п. 1.5, электрическая составляющая оказывает гораздо большее воздействие на вещество. Поэтому в оптике принято рассматривать сложение векторов 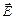, которые называют световыми. Итак,

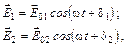(3.1.1)

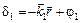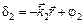где величины и характеризуют фазы колебаний в данной точке пространства с радиус-векторм 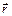, но не зависят от времени.

Амплитуду 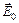результирующего вектора 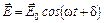легко найти с помощью метода векторных диаграмм. Из рисунка видно, что длина вектора 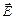определяется по теореме косинусов

. (3.1.2)

Энергия световой волны пропорциональна квадрату вектора напряженности электрического поля. Введем новую величину

, (3.1.3)

называемую интенсивностью света. Усреднение необходимо проводить по времени разрешения приемника. Но так как эти времена гораздо больше периода колебаний, усреднение достаточно провести по периоду. В результате усреднения интенсивность света будет пропорциональна амплитуде колебаний, т.е. 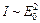. Запишем уравнение (3.1.2) через величину I

.

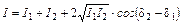Усредним полученное выражение по времени

.

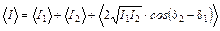Считая, что амплитуды исходных колебаний не зависят от времени, можно записать

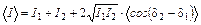. (3.1.4)

Анализ формулы (3.1.4) приводит к следующим результатам:

– если 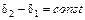, то

.

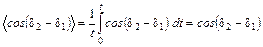Тогда выражение (3.1.4) принимает вид

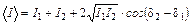. (3.1.5)

То есть, интенсивность результирующих колебаний отличается от простой суммы интенсивностей исходных колебаний. Третье слагаемое в выражении (3.1.5) называют интерференционным;

– если же 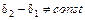, т.е. принимает всевозможные значения, то 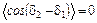. В этом случае интерференция отсутствует.

Соотношение (3.1.5) показывает, что интенсивность результирующих колебаний зависит не только от интенсивности складываемых волн, но и от величины 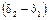, называемой сдвигом фаз. Если d₁ и d₂ равны или отличаются на 2 m p (m – целое число), то интенсивность будет максимальна. Если же d₁ и d₂ отличаются на (2 m +1)p, то интенсивность будет минимальна. Распишем выражение для сдвига фаз

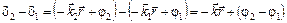, (3.1.6)

где .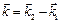

Выражения (3.1.5) и (3.1.6) показывают, что интенсивность света меняется по синусоидальному закону. Поверхности одинаковых интенсивностей представляют собой плоскости, перпендикулярные вектору . Расстояние D х между соседними плоскостями равной интенсивности находятся из условия k × D x = 2p. Так как длины векторов и 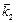одинаковы 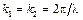, то

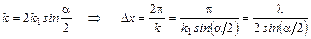. (3.1.7)

Для малых углов a формула (3.1.7) принимает вид .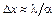

Если поставить плоский экран параллельно вектору 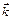, то на экране появятся светлые и темные интерференционные полосы. Расстояние D x в этом случае называется шириной интерференционной полосы.