
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Интерференция в тонких пленках. Особый случай двулучевой интерференции представляет интерференция в тонких пленках и пластинках
|
|
Особый случай двулучевой интерференции представляет интерференция в тонких пленках и пластинках. В отличае от рассмотренных в п. 3.6., интерференция в тонких пленках – это способ получения когерентных пучков делением амплитуды. Разделяют два вида такой интерференции: на плоскопараллельных пластинках и на пластинках переменной толщины.
 Интерференция в тонких пленках возникает при отражении от верхней и нижней ее поверхностей. Луч света l 1 от источника S падает на плоскопараллельную пластинку толщиной h с показателем преломления n 2 под углом a. На верхней границе раздела он частично отражается под тем же углом a и частично преломляется под углом b. Преломленный луч l 3, отражаясь от нижней границы раздела и преломляясь на верхней границе, следует параллельно лучу l 2. Если на пути лучей l 2 и l 3 поставить собирающую линзу, то в фокальной плоскости этой линзы они будут интерферировать. Интерференция лучей l 2 и l 3 называется интерференцией в отраженном свете. Лучи l 4 и l 5 также выходят параллельно друг другу и могут интерферировать. Такую интерференцию называют интерференцией в проходящем свете.
Интерференция в тонких пленках возникает при отражении от верхней и нижней ее поверхностей. Луч света l 1 от источника S падает на плоскопараллельную пластинку толщиной h с показателем преломления n 2 под углом a. На верхней границе раздела он частично отражается под тем же углом a и частично преломляется под углом b. Преломленный луч l 3, отражаясь от нижней границы раздела и преломляясь на верхней границе, следует параллельно лучу l 2. Если на пути лучей l 2 и l 3 поставить собирающую линзу, то в фокальной плоскости этой линзы они будут интерферировать. Интерференция лучей l 2 и l 3 называется интерференцией в отраженном свете. Лучи l 4 и l 5 также выходят параллельно друг другу и могут интерферировать. Такую интерференцию называют интерференцией в проходящем свете.
Для расчета интерференционной картины в отраженном свете найдем оптическую разность хода лучей l 2 и l 3. Предположим, что первая среда – воздух, то есть n 1» 1. Тогда, обозначив n 2 = n, для оптической разности хода получим следующее выражение
 . (3.7.1)
. (3.7.1)
Из рисунка видно, что  и
и  связаны с толщиной пластинки h и углом преломления b соотношением
связаны с толщиной пластинки h и углом преломления b соотношением  , а
, а
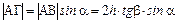 .
.
Учитывая закон преломления  , получаем
, получаем
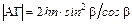 . Тогда
. Тогда
 . (3.7.2)
. (3.7.2)
В уравнение (3.7.2) необходимо ввести поправку. В пределе, когда толщина пластинки стремится к нулю, выражение для разности хода обращается в нуль. Поэтому в отраженном свете должно было бы происходить усиление колебаний. Но это невозможно, так как бесконечно тонкая пластинка вообще не может оказывать никакого действия на распространение света. Для этого волны, отраженные от верхней и нижней поверхностей пластинки, должны при интерференции гасить друг друга. Дело в том, что свет, отраженный от оптически более плотной среды, изменяет фазу на p. Более подробное обоснование данного явления будет приведено в п. 5.3. Таким образом, к разности хода необходимо прибавить или отнять l/2. Кроме того, 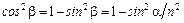 . Поэтому полная разность хода будет выглядеть следующим образом:
. Поэтому полная разность хода будет выглядеть следующим образом:
 . (3.7.3)
. (3.7.3)
В соответствии с формулой (3.7.3), светлые полосы расположены в местах, для которых
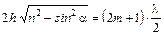 , (3.7.4)
, (3.7.4)
а темные в местах, для которых
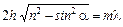 , (3.7.5)
, (3.7.5)
где m – целое число, называемое порядком интерференции. Как следует из формул (3.7.4) и (3.7.5), при фиксированных значениях длины волны, толщине пластинки и ее показателя преломления каждому значению угла падения a соответствует своя интерференционная полоса. Поэтому такие полосы называют интерференционными полосами равного наклона.
В проходящем свете геометрическая разность хода между лучами l 4 и l 5 такая же, как и для лучей l 2 и l 3. Однако, ни один из них не отражается от оптически более плотной среды. Таким образом, оптическая разность хода определяется соотношением
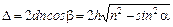 .
.
То есть, условие минимума интерференционной картины определяется соотношением (3.7.4), а условие максимума – формулой (3.7.5).