
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Многолучевая интерференция. До сих пор мы рассматривали интерференцию от двух когерентных источников
|
|
До сих пор мы рассматривали интерференцию от двух когерентных источников. Однако, часто на практике приходится иметь дело с наложением волн от нескольких источников. Рассмотрим один из таких случаев более подробно.
 Пусть на плоскопараллельную пластинку толщиной h падает пучок света под углом a. Мы видим, что этот пучок может многократно отражаться от верхней и нижней граней пластинки. Обозначим через R коэффициент отражения света на границе раздела " пластинка-воздух", то есть долю энергии падающего света, которая возвращается обратно при каждом отражении. При отсутствии поглощения оставшаяся доля (1 – R) проходит через границу раздела. Если среды по обе стороны пластинки одинаковы, то коэффициенты отражения на обеих поверхностях пластинки будут одинаковы. Обозначим через I 0 интенсивность падающего пучка,
Пусть на плоскопараллельную пластинку толщиной h падает пучок света под углом a. Мы видим, что этот пучок может многократно отражаться от верхней и нижней граней пластинки. Обозначим через R коэффициент отражения света на границе раздела " пластинка-воздух", то есть долю энергии падающего света, которая возвращается обратно при каждом отражении. При отсутствии поглощения оставшаяся доля (1 – R) проходит через границу раздела. Если среды по обе стороны пластинки одинаковы, то коэффициенты отражения на обеих поверхностях пластинки будут одинаковы. Обозначим через I 0 интенсивность падающего пучка,
тогда для пучков l 2, l 4, l 6,... запишем:
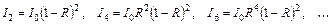 ,
,
а соответствующие амплитуды
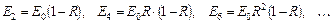 .
.
Разность хода между соседними пучками 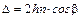 , а разность фаз
, а разность фаз 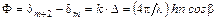 . Тогда комплексную амплитуду прошедшей волны можно представить в виде убывающей геометрической прогрессии
. Тогда комплексную амплитуду прошедшей волны можно представить в виде убывающей геометрической прогрессии
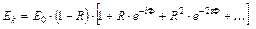 . (3.10.1)
. (3.10.1)
Если пластинка достаточно длинная, то прогрессию можно считать бесконечной, т.е.
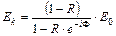 .
.
Интенсивность прошедшей волны будет равна
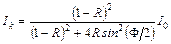 . (3.10.2)
. (3.10.2)
Аналогично можно рассчитать интенсивность света и для отраженной волны
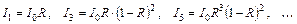
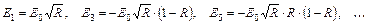
Знак " –" учитывает потерю полуволны на одной из поверхностей пластинки. Для результирующей амплитуды
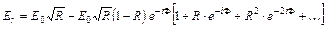 ,
,
или
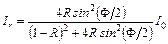 . (3.10.3)
. (3.10.3)
Если сложить интенсивности Ik и Ir , то (при отсутствии поглощения) результат будет равен I 0. Для получения интерференционной картины приходится пользоваться протяженными источниками. Полосы интерференции будут полосами равного наклона. Максимумы интенсивности в проходящем свете получаются при выполнении  условия
условия 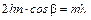 , где m – целое число. В отраженном свете этим местам соответствуют минимумы. Если коэффициент отражения мал (R < < 1), тогда в формулах (3.10.2) и (3.10.3) можно пренебречь слагаемыми с R 2 и произвести разложение в ряд по R
, где m – целое число. В отраженном свете этим местам соответствуют минимумы. Если коэффициент отражения мал (R < < 1), тогда в формулах (3.10.2) и (3.10.3) можно пренебречь слагаемыми с R 2 и произвести разложение в ряд по R
 или
или 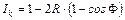 ;
;
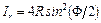 или
или 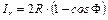 .
.
Но при увеличении коэффициента отражения R распределение существенно меняется. При R ® 1 весь свет практически сосредотачивается в очень узких полосах на темном фоне.