
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Влияние температуры на скорость химических реакций
|
|
С повышением температуры скорость реакции, как правило, возрастает, а концентрация веществ от температуры не зависит, следовательно, повышение скорости происходит за счет увеличения константы скорости. Количественно эта зависимость определяется основным уравнением химической кинетики Аррениуса:
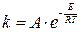 , (12)
, (12)
где A – предэкспоненциальный множитель, постоянный для конкретной реакции; E – энергия активации реакции, которая означает избыток энергии сверх средней, которым должны обладать молекулы, чтобы при столкновении между ними могло произойти химическое взаимодействие.
Таким образом, энергия активации это энергетический барьер, который должны преодолеть взаимодействующие частицы. Очевидно, чем выше этот барьер, тем меньше активных, т.е. способных к взаимодействию частиц и скорость процесса будет ниже. При значительной величине E может случиться, что в течение длительного времени не найдется ни одной пары частиц, способных к взаимодействию; в таком случае говорят о заторможенности процесса по кинетическим причинам. Так как энергия активации есть избыток энергии сверх средней, то по своему смыслу она не может быть отрицательной (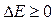 ) и если она приближается к нулю, то, следовательно, для взаимодействия не требуется избытка энергии и большинство молекул, обладающих средним запасом энергии, будут активными. В этом случае скорость процесса максимальна и практически не будет зависеть от температуры. Энергия активация есть вторая важная характеристика процесса. Логарифмируя уравнение 3 и дифференцируя по Т (при условии, что Е и A не зависят от температуры), получим:
) и если она приближается к нулю, то, следовательно, для взаимодействия не требуется избытка энергии и большинство молекул, обладающих средним запасом энергии, будут активными. В этом случае скорость процесса максимальна и практически не будет зависеть от температуры. Энергия активация есть вторая важная характеристика процесса. Логарифмируя уравнение 3 и дифференцируя по Т (при условии, что Е и A не зависят от температуры), получим:
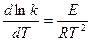 . (13)
. (13)
Поскольку Е> 0, то с повышением температуры константа скорости любой реакции возрастает, причем тем более интенсивно, чем выше величина Е. При Е ® 0, k ® A таким образом скорость реакции перестает зависеть от температуры.
Интегрируя (13) при Е= сonst, получим выражение
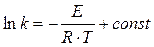 . (14)
. (14)
В координатах ln k – 1/T эта зависимость выражается прямой, тангенс угла наклона которой позволяет определить величину Е из экспериментальных данных. Интегрирование выражения 4 в пределах от Т1 до Т2 приводит к соотношению 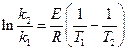 , из которого находят энергию активации процесса:
, из которого находят энергию активации процесса:
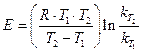 . (15)
. (15)
Выражение (15) позволяет вычислить энергию активации по двум значениям констант скоростей k1 и k2, полученных при двух температурах Т1 и Т2.