
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Непрерывной случайной величины
|
|
НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ
Методические указания к практическим занятиям
по дисциплине «Высшая математика»
Составители: Ю.Б. Егорова
И.М. Мамонов
А.В. Челпанов
МОСКВА 2006
ВВЕДЕНИЕ
Методические указания предназначены для студентов дневного и вечернего отделения факультета №14 специальностей 150601, 160301, 230102. Указания выделяют основные понятия темы, определяют последовательность изучения материала. Большое количество рассмотренных примеров помогает в практическом освоении темы. Методические указания служат основой для практических занятий и выполнения индивидуальных заданий.
НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ
НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
1.1.Нормальный закон распределения (закон Гаусса) наиболее часто встречается на практике. Он появляется в тех случаях, когда непрерывная случайная величина является результатом влияния большого числа факторов.
Примеры случайных величин, имеющих нормальный закон распределения: ошибки измерений; отклонения при стрельбе; отклонение размеров деталей от номинальных при их изготовлении; рост, вес людей; температура воздуха, тела, объекта и т.п.
1.2. Плотность распределения вероятностей (дифференциальная функция распределения) имеет вид:
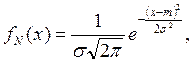
где m и s - параметры нормального распределения: m = М (Х) - математическое ожидание случайной величины Х, s = s (Х) - среднее квадратическое отклонение.
Если параметры распределения известны, функция fN(х) полностью определена. Для сокращенной записи того, что непрерывная случайная величина Х имеет нормальный закон распределения с параметрами m и s, принято условное обозначение Х~N(m, s).
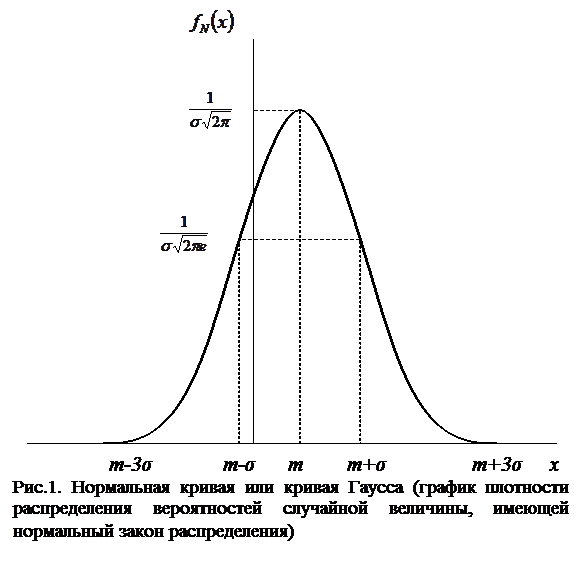
График функции fN(х) называется нормальной кривой или кривой Гаусса (рис.1).
Функция fN(х) и нормальная кривая имеют следующие свойства:
1) Область определения функции fN(х) - вся числовая ось (-µ; +µ);
2) Функция fN(х) может принимать только положительные значения: fN(х)> 0, т.е. нормальная кривая расположена над осью 0 x;
3) Ось 0 х - горизонтальная асимптота нормальной кривой;
4) Нормальная кривая симметрична относительно прямой х=m;
5) При х=m нормальная кривая имеет максимум:
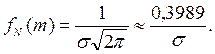
6) При хп=m ± s нормальная кривая имеет перегиб:
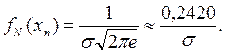
1.3.Интегральная функция распределения вероятностей нормальной случайной величины:
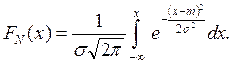
График функции FN(х) приведен на рис.2.
Свойства интегральной функции распределения нормальной случайной величины:
1) Функция FN(x) есть неубывающая и непрерывная функция;
2) Функция FN(x) есть неотрицательная функция, заключенная между нулем и единицей: 0£ FN(x)£ 1;
3) FN(-µ) =0; FN(+Ґ) = 1;
4) При х = m функция FN(х)= 0, 5.
 | |||
 |
1.4.Числовые характеристики нормальной случайной величины:
Mатематическое ожидание, мода и медиана совпадают и равны m:
M(X)=Мо=Ме = m.
Дисперсия D(X) =s2.
Среднее квадратическое отклонение s(Х)=s.
Коэффициент ассиметрии А =0.
Коэффициент эксцесса e= 3, эксцесс Е=e–3 =0.
1.5.Вероятность попадания в заданный интервал: вероятность того, что нормальная случайная величина Х попадет в заданный интервал (a, b), равна:
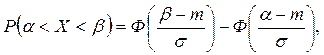
где Ф(z) - функция Лапласа. Свойства функции Лапласа приведены ниже (см. п.2).
1.6.Вероятность заданного отклонения: вероятность того, что нормальная случайная величина Х отклонится от математического ожидания на величину, меньшую d, равна:
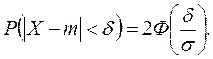
1.7. Правило «3 s». Если случайная величина Х имеет нормальный закон распределения, то практически достоверно, что все ее значения находятся в " трех- s " интервале (m -3 s, m +3 s):
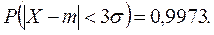
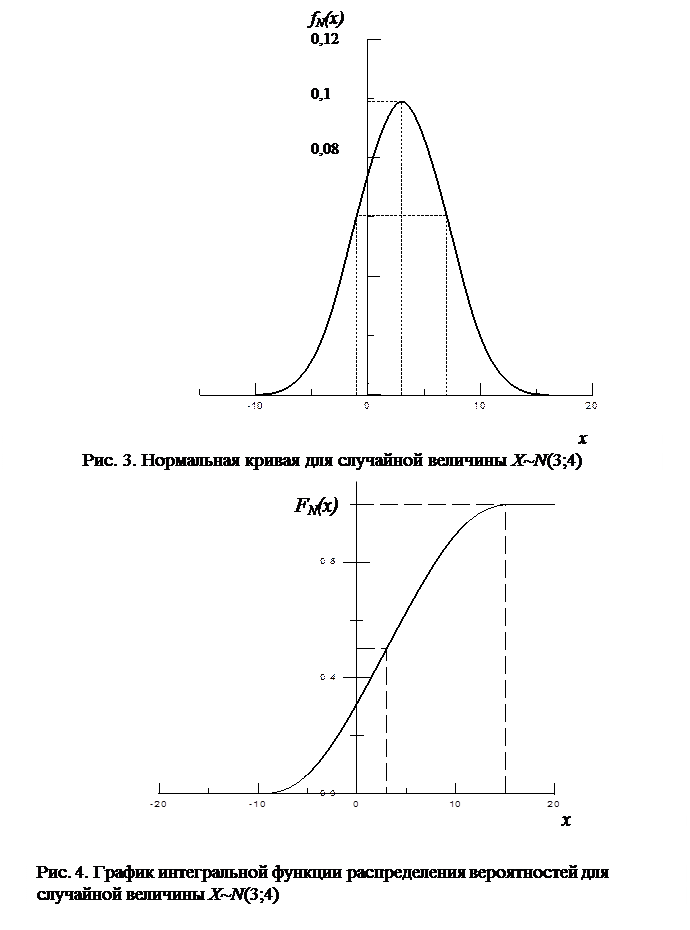
ПРИМЕР 1. Найти интегральную и дифференциальную функции распределения, если непрерывная случайная величина Х имеет нормальный закон распределения с параметрами: m =3, s =4. Построить нормальную кривую и график интегральной функции распределения. Найти числовые характеристики.
Решение. Плотность распределения вероятностей (дифференциальная функция распределения) имеет вид:
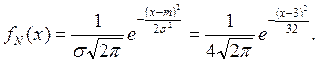
Интегральная функция распределения:
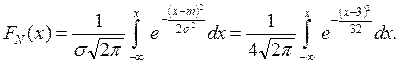
Для построения нормальной кривой используем свойства функции fN(x) и правило «3 s»:
1) Область определения функции fN(х) - вся числовая ось (-µ; +µ).
2) Так как функция fN(х) может принимать только положительные значения fN(х)> 0, то нормальная кривая расположена над осью 0 х.
3) Ось 0 х - горизонтальная асимптота нормальной кривой.
4) Нормальная кривая симметрична относительно прямой х=m= 3.
5) Приблизительно все значения х заключены в трехсигмовом интервале: [ m –3 s; m +3 s ]=[3–3× 4; 3+3× 4]=[-9; 15].
6) При х=m =3 нормальная кривая имеет максимум:
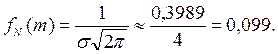
7) При хп=m ± s =3±4=-1; 7 нормальная кривая имеет перегиб:
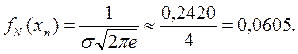
График функции fN(x) (нормальная кривая) представлен на рис.3.
Для построения графика интегральной функции распределения используются свойства функции FN (x) и правило «3 s»:
1) Функция FN(x) есть неубывающая и непрерывная функция.
2) Функция FN(x) есть неотрицательная функция, заключенная между нулем и единицей: 0£ FN(x)£ 1.
3) FN(-µ) =0; FN(+Ґ) = 1.
4) При х = m =3 функция FN(х)= 0, 5.
5) Приблизительно все значения х заключены в трехсигмовом интервале: [ m –3 s; m +3 s ]=[3–3× 4; 3+3× 4]=[-9; 15].
График функции FN (x) приведен на рис.4.
Числовые характеристики нормальной случайной величины:
Mатематическое ожидание, мода и медиана: M(X)=Мо=Ме = m= 3.
Дисперсия D(X) =s2 =16.
Среднее квадратическое отклонение s(Х)=s =4.
Коэффициент ассиметрии А =0.
Коэффициент эксцесса e= 3, эксцесс Е=e-3 =0.