Задачи для самостоятельного решения

1. Математическое ожидание нормально распределенной случайной величины Х равно 3. Среднее квадратическое отклонение равно 2. Написать плотность распределения вероятности и интегральную функцию распределения вероятности случайной величины Х. Найти дисперсию, моду, медиану, коэффициент асимметрии и эксцесс.

2. Нормально распределенная случайная величина Х задана плотностью распределения вероятностей:

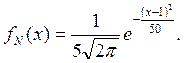
Найти интегральную функцию распределения вероятностей, определить математическое ожидание и дисперсию случайной величины Х. Построить нормальную кривую.

3. Параметры нормально распределенной случайной величины Х равны m =20 и σ =5. Найти интегральную и дифференциальную функции распределения. Построить их графики. Найти числовые характеристики. Определить вероятность того, что в результате испытания Х примет значение, заключенное в интервале (15; 25). Проиллюстрировать решение задачи графически.

4. Автомат штампует детали. Контролируется длина детали Х, которая распределена нормально с математическим ожиданием (проектной длиной), равным 50 мм. Фактически длина изготовленных деталей не менее 32 и не более 68 мм. Найти вероятность того, что длина наудачу взятой детали: а) больше 55 мм; б) меньше 40 мм. Проиллюстрировать решение задачи графически.(Указание: из равенства Р (32< Х < 68)=1 предварительно найти σ).

5. Производится взвешивание некоторого вещества без систематических ошибок. Случайные ошибки взвешивания подчинены нормальному закону со средним квадратическим отклонением 20 г. Найти вероятность того, что взвешивание будет произведено с ошибкой, не превосходящей по абсолютной величине 10 г. Проиллюстрировать решение задачи графически.

6. Деталь, изготовленная автоматом, считается годной, если отклонение ее контролируемого размера от проектного не превышает 10 мм. Случайные отклонения контролируемого размера от проектного подчинены нормальному закону с параметрами m =0 мм и σ =5 мм. Сколько процентов годных деталей изготавливает автомат?

7. Случайная величина Х (длина детали) распределена нормально с математическим ожиданием 25 мм. Вероятность попадания Х в интервал (10; 15) равна 0, 2. Чему равна вероятность попадания Х в интервал (35; 40)? Проиллюстрировать решение задачи схематически.

8. Параметры нормально распределенной случайной величины Х (диаметр валиков) равны m =10 мм и σ =0, 1 мм. Написать интегральную и дифференциальную функции распределения. Найти интервал, симметричный относительно математического ожидания, в котором с вероятностью 0, 9973 будут заключены диаметры изготовленных валиков. Как называется этот интервал?

9. Случайная величина Х имеет нормальный закон распределения с параметром σ =5. Найти длину интервала, симметричного относительно математического ожидания, в который с вероятностью 0, 9973 попадет Х в результате испытания.

10. Непрерывная случайная величина Х имеет нормированный нормальный закон распределения. Найти «3 σ»-интервал. Определить вероятность того, что случайная величина Х попадет в интервал (1; 3). Проиллюстрировать решение задачи графически.

11. Отклонение стрелки компаса из-за влияния магнитного поля в определенной области Заполярья есть случайная величина Х ~ N (0; 1). Чему равна вероятность того, что абсолютная величина отклонения стрелки компаса в определенный момент времени будет больше, чем 2, 4? Проиллюстрировать решение задачи графически.

12. Дневная добыча угля в некоторой шахте распределена по нормальному закону с параметрами m =785 т и σ =60 т. Найти вероятность того, что в определенный день будут добыты: а) по крайней мере 800 т угля; б) менее 665 т.

13. Вес грейпфрута, выращенного в Краснодарском крае, – нормально распределенная случайная величина с неизвестным математическим ожиданием и дисперсией, равной 0, 04 кг². Агрономы знают, что 65% фруктов весят меньше, чем 0, 5 кг. Найти ожидаемый вес случайно выбранного грейпфрута.

14. Вес товаров в контейнерах – есть нормально распределенная случайная величина. Известно, что 65% контейнеров с товаром имеют вес больше, чем 4, 9 т, а 25% – имеют вес меньше, чем 4, 2 т. Найти ожидаемый средний вес и среднее квадратическое отклонение веса контейнера.

15. Случайные ошибки измерения подчинены нормальному закону с параметрами m =0 и σ =20 мм. Найти вероятность того, что из трех независимых измерений ошибка хотя бы одного не превзойдет по абсолютной величине 4 мм.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какая величина называется случайной?

2. Дайте определение непрерывной случайной величины.

3. Что называется законом распределения непрерывной случайной величины?

4. Дайте определение дифференциальной и интегральной функции распределения вероятностей.

5. Какое распределение вероятностей называется нормальным?

6. Сформулируйте свойства дифференциальной функции (плотности) распределения вероятностей нормальной случайной величины Х.

7. Сформулируйте свойства интегральной функции распределения вероятностей нормальной случайной величины Х.

8. Чему равны числовые характеристики случайной величины, имеющей нормальное распределение?

9. Сформулируйте правило «3σ».

10.Сформулируйте свойства функции Лапласа.

11.Как можно найти вероятность попадания нормальной случайной величины Х в заданный интервал (α, β)?

12.Как можно найти вероятность заданного отклонения δ нормальной случайной величины Х от ее математического ожидания?

13. Какое распределение вероятностей называется нормальным нормированным распределением?

14.Чему равны числовые характеристики случайной величины, имеющей нормированное нормальное распределение?

15. Приведите примеры случайных величин, имеющих нормальное распределение.

ЛИТЕРАТУРА

1. Гмурман В.С. Теория вероятностей и математическая статистика. -7-е изд., стер. -М.: Высш. шк. 2001.-479 с.

2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. -5-е изд., стер.– М.: Высш. шк. 2001. -400 с.

3. Колде Я.К. Практикум по теории вероятностей и математической статистике. – М.: Высш. шк., 1991. -157 с.

4. Кремер Н.Ш. Теория вероятностей и математическая статистика. -М.: ЮНИТИ-ДАНА, 2001. -543 с.

5. Егорова Ю.Б., Мамонов И.М., Корниенко Л.И. Дискретные случайные величины. Методические указания к практическим занятиям по дисциплине «Высшая математика». – М.: Издательский центр МАТИ, 2005. – 20 с.