Функция Лапласа. Ее свойства

2.1. Функция (интеграл вероятностей) Лапласа имеет вид:

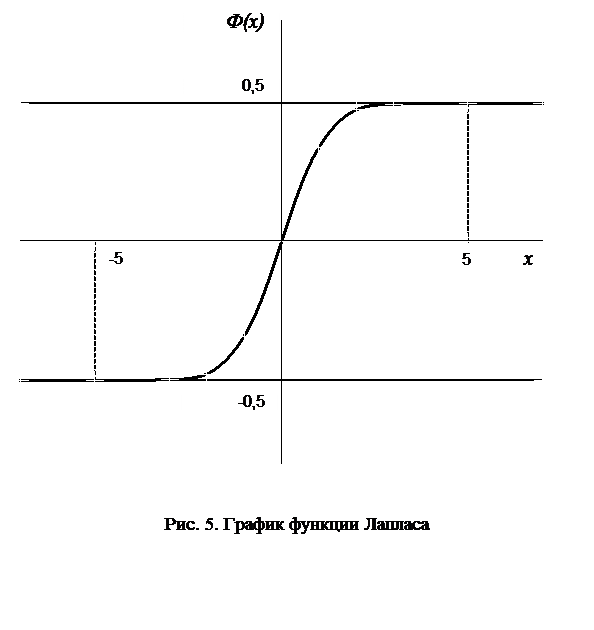
График функции Лапласа приведен на рис.5.

Функция Ф (х) табулирована (см. табл. 1 приложений). Для применения этой таблицы нужно знать свойства функции Лапласа:

1) Функция Ф(х) нечетная: Ф (- х)= - Ф (х).

2) Функция Ф (х) монотонно возрастающая.

3) Ф (0)=0.

4) Ф (+¥)=0, 5; Ф (-¥)=-0, 5. На практике можно считать, что при х³ 5 функция Ф (х)=0, 5; при х£ -5 функция Ф (х)=-0, 5.

2.2. Существует другие формы функции Лапласа:

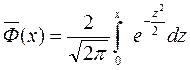и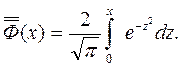

В отличие от этих форм функция Ф (х) называется стандартной или нормированной функцией Лапласа. Она связана с другими формами соотношениями:

ПРИМЕР 2. Непрерывная случайная величина Х имеет нормальный закон распределения с параметрами: m =3, s =4. Найти вероятность того, что в результате испытания случайная величина Х: а) примет значение, заключенное в интервале (2; 6); б) примет значение, меньше 2; в) примет значение, больше 10; г) отклонится от математического ожидания на величину, не превышающую 2. Проиллюстрировать решение задачи графически.

Решение. а) Вероятность того, что нормальная случайная величина Х попадет в заданный интервал (a, b), где a =2 и b =6, равна:

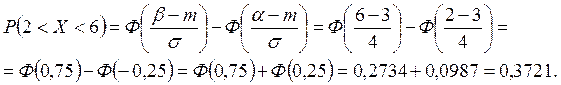
Значения функции Лапласа Ф(х) определяют по таблице, приведенной в приложении, учитывая, что Ф (– х)= – Ф (х).

б) Вероятность того, что нормальная случайная величина Х примет значение меньше 2, равна:

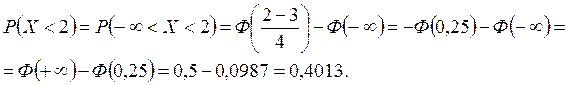
в) Вероятность того, что нормальная случайная величина Х примет значение больше 10, равна:

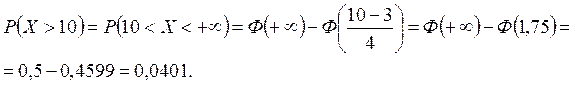
г) Вероятность того, что нормальная случайная величина Х отклонится от математического ожидания на величину, меньшую d =2, равна:

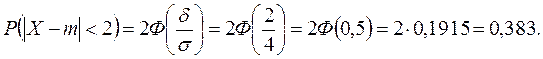
С геометрической точки зрения, вычисленные вероятности численно равны заштрихованным площадям под нормальной кривой (см. рис.6).

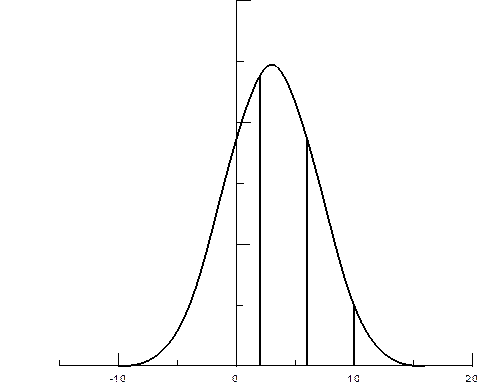
Рис. 6. Нормальная кривая для случайной величины Х ~ N (3; 4)
ПРИМЕР 3. Производится измерение диаметра вала без систематических (одного знака) ошибок. Случайные ошибки измерения подчинены нормальному закону распределения со средним квадратическим отклонением 10 мм. Найти вероятность того, что измерение будет произведено с ошибкой, не превышающей по абсолютной величине 15 мм.

Решение. Математическое ожидание случайных ошибок равно нулю m =0. Тогда вероятность того, что нормальная случайная величина Х отклонится от математического ожидания на величину, меньшую d =15, равна:

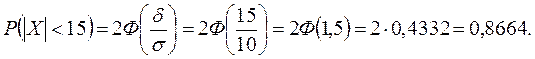
ПРИМЕР 4. Автомат изготовляет шарики. Шарик считается годным, если отклонение Х диаметра шарика от проектного размера по абсолютной величине меньше 0, 7 мм. Считая, что случайная величина Х распределена нормально со средним квадратическим отклонением 0, 4 мм, найти, сколько в среднем будет годных шариков среди 100 изготовленных.

Решение. Случайная величина Х - отклонение диаметра шарика от проектного размера. Математическое ожидание отклонения равно нулю, т.е. М (Х)= m =0. Тогда вероятность того, что нормальная случайная величина Х отклонится от математического ожидания на величину, меньшую d =0, 7, равна:

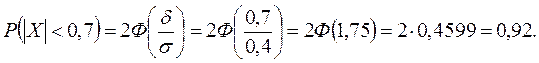
Отсюда следует, что примерно 92 шарика из 100 окажутся годными.

ПРИМЕР 5. Доказать правило «3 s».

Решение. Вероятность того, что нормальная случайная величина Х отклонится от математического ожидания на величину, меньшую d= 3 s, равна:

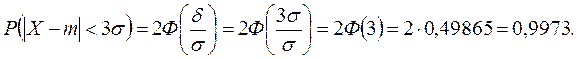
ПРИМЕР 6. Случайная величина Х распределена нормально с математическим ожиданием m =10. Вероятность попадания Х в интервал (10, 20) равна 0, 3. Чему равна вероятность попадания Х в интервал (0, 10)?

Решение. Нормальная кривая симметрична относительно прямой х = m =10, поэтому площади, ограниченные сверху нормальной кривой и снизу интервалами (0, 10) и (10, 20), равны между собой. Так как площади численно равны вероятностям попадания Х в соответствующий интервал, то: