
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Упражнения. Модуль 4. Линейные операторы
|
|
Модуль 4. Линейные операторы. Квадратичные формы
Глава 4.1. Линейные операторы
Линейные операторы в линейном пространстве
Линейным оператором, действующим в линейном пространстве V над полем K, называется отображение 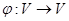 , для которого
, для которого
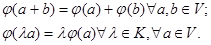
Свойства линейного оператора
1) 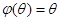 , где
, где 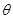 – нулевой вектор линейного пространства V/K;
– нулевой вектор линейного пространства V/K;
2) 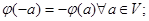
3) 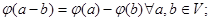
4) 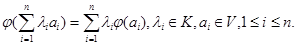
Доказательство.
1) 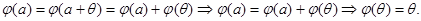
2) 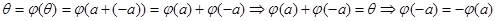
3) 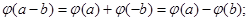
4) 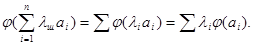
Примеры.
1)Нулевой линейный оператор, который каждый элемент линейного пространства переводит в нулевой вектор.
2) Тождественный линейный оператор, который каждый элемент линейного пространства переводит в себя.
Упражнения
1) Является ли линейным оператор, действующий в трехмерном евклидовом пространстве геометрических векторов:
а) 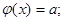 б)
б) 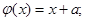 в)
в) 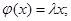 г)
г) 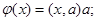
д) 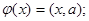 е)
е) 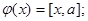 ё)
ё) 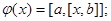
где а – фиксированный вектор, 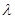 – число, (х, а) – скалярное произведение.
– число, (х, а) – скалярное произведение.
2) Является ли линейным оператор, действующий в трехмерном арифметическом пространстве:
а) 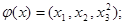 б)
б) 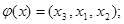 в)
в) 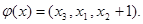
3) Докажите, что  – линейный оператор одномерного линейного пространства над полем K тогда и только тогда, когда существует элемент
– линейный оператор одномерного линейного пространства над полем K тогда и только тогда, когда существует элемент 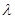 из поля K, для которого
из поля K, для которого 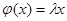 , где х – любой вектор этого линейного пространства.
, где х – любой вектор этого линейного пространства.
4) Какие из отображений являются линейными операторами линейного пространства многочленов степени 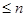
а)  б)
б) 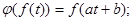 в)оператор дифференцирования
в)оператор дифференцирования 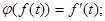 г)оператор k -кратного дифференцирования
г)оператор k -кратного дифференцирования 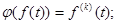 д)
д) 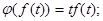 е)
е) 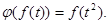
5) Линейное пространство Х является прямой суммой подпространств L 1 и L 2. Докажите, что оператор Р проектирования линейного пространства Х на L 1 параллельно L 2, который каждому вектору х 1 + х 2 из Х ставит в соответствие вектор х 1, линейный; х 1  х 2
х 2 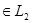 .
.
6) Линейное пространство Х является прямой суммой подпространств L 1 и L 2. Докажите, что оператор R отражения линейного пространства Х на L 1 параллельно L 2, который каждому вектору х 1 + х 2 из Х ставит в соответствие вектор х 1 – х 2, линейный; х 1  х 2
х 2 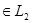 .
.
7) В линейном пространстве Х над полем K фиксирован базис 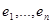 . Докажите, что соответствие, относящее каждому вектору Х линейного пространства его i- ю координату в этом базисе, линейное отображение из Х в K.
. Докажите, что соответствие, относящее каждому вектору Х линейного пространства его i- ю координату в этом базисе, линейное отображение из Х в K.
8) Докажите, что линейный оператор, действующий в одномерном линейном пространстве над полем K, сводится к умножению вектора пространства на фиксированный элемент поля.
9) Докажите, что линейный оператор линейно зависимую систему переводит в линейно зависимую. Верно ли аналогичное утверждение для линейно независимой системы векторов?
10) Верно ли утверждение: линейный оператор эквивалентные системы переводит в эквивалентные?