Сумма и произведение линейных операторов

Суммой двух линейных операторов и 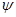называется оператор 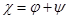, для которого .

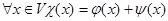Теорема. Если и 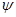– линейные операторы, действующие в линейном пространстве V, то + 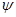– также линейный оператор, действующий в V. Если А и В – матрицы линейных операторов и 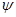в базисе е, то матрица суммы этих линейных операторов в базисе е равна А + В.

Доказательство. Непосредственно проверяется. ■

Произведением 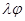линейного оператора на элемент 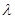из поля K называется оператор h = 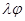, для которого .

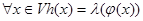Теорема. Если 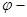линейный оператор, действующий в линейном пространстве V / K, то 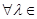K оператор 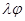– также линейный. Матрица линейного оператора 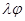в базисе е равна матрице линейного оператора в этом базисе, умноженной на .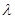

Доказательство. Непосредственно проверяется. ■

Теорема. Множество U всех линейных операторов, действующих в линейном пространстве V размерности n над полем K, относительно введенных действий сложения и умножения на элемент поля K образует линейное пространство над полем K размерности n ².

Доказательство проводится непосредственной проверкой всех аксиом линейного пространства. ■

Произведением линейных операторов и 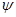, действующих в линейном пространстве V/K, называется оператор g = , для которого 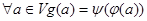. Определим также .

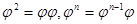Теорема. Если и 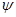линейные операторы, действующие в линейном пространстве V/K, то – также линейный оператор. Матрица линейного оператора в базисе е равна произведению матрицы А линейного оператора на матрицу В линейного оператора .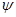

Доказательство. ()(е) = 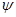(Ае) = А 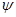е 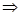= АВе ()(е) = АВе. ■

Для ненулевого многочлена f(t) = 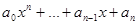значение многочлена от линейного оператора f(А) = 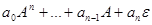, где 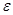– тождественное отображение.

Теорема. Гамильтона-Кэли. Линейный оператор является корнем своего характеристического многочлена.

Теорема была доказана для матриц. Здесь мы переформулировали ее для линейных операторов. ■