Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Ядро и образ линейного оператора
|
|
Ядром линейного оператора 
называется множество всех элементов линейного пространства, которые линейный оператор отображает в нулевой вектор, т.е.
.
Ядро не пусто, так как содержит нулевой вектор. Ясно, что ядро – подпространство линейного пространства. Размерность этого подпространства называют дефектом линейного оператора.
Образом линейного оператора называется множество всех элементов у из V, для которых существует вектор х такой, что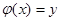 
, т.е.
.
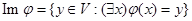Образ не пуст, так как содержит нулевой вектор. Ясно, что образ – подпространство линейного пространства. Размерность этого подпространства называют рангом линейного оператора.
Теорема. Сумма размерностей ядра и образа линейного оператора равна размерности линейного пространства.
Доказательство. Пусть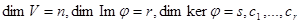 
– базис 
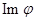, a 1, …, as – базис 
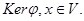Тогда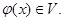 
Следовательно, можно записать
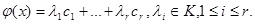
По определению 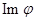в линейном пространстве существуют элементы b 1, …, br, для которых 
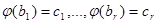. Отсюда,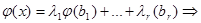 
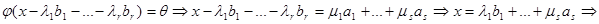a 1, …, as, b 1, …, br – система образующих линейного пространства.
Докажем линейную независимость этих векторов. Пусть
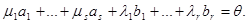
Подействуем нашим линейным оператором на обе части равенства. Получим
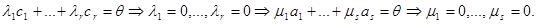
Система образующих a 1, …, as, b 1, …, br линейно независима, т.е. образует базис линейного пространства V/ K., поэтому s + r = n. ■