Дисперсия — это средний квадрат отклонения всех значе­ний признака ряда распределения от средней арифметической.

Именно дисперсия и среднее квадратическое отклонение явля­ются основными наиболее употребляемыми показателями вариации.

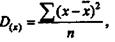
Обозначается дисперсия буквой

где х — значение признака;

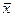- средняя арифметическая;

п — численность совокупности.

Но

Поделив это выражение на п, учтем, что 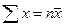. Тогда

т. е. дисперсия равна разности среднего квадрата вариантов и квад­рата их средней (подразумевая здесь под " средней" среднюю ариф­метическую). И, наконец,

Заменяя в формуле определения дисперсии (D_x) среднее суммами, разделенными на численность совокупности, получим формулу:

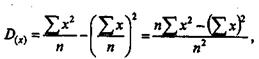
имеющую некоторые технические преимущества для ее вычисле­ния. При ее применении округление производится только один раз и в самом конце вычисления.

Пример. В табл. 15 приведены данные для расчета дисперсии и среднего квадратического отклонения на примере стажа продав­цов торговой фирмы " Элегант", работающих в двух ее магазинах.

Для 1-го магазина:

Таблица.15

Данные для расчета дисперсии и среднего квадратического отклонения по стажу продавцов в двух магазинах фирмы " Элегант"

п/п	1-й магазин	2-й магазин
Стаж продавцов, лет (x)	отклонения от среднего	Квадрат отклонения	Стаж продавцов, лет (x)	отклонения от среднего	Квадрат отклонения
		-6, 2	38, 44		-1, 2	1, 44
		-5, 2	27, 04		-1, 2	1, 44
		-4, 2	17, 64		-0, 2	0, 04
		-4, 2	17, 64		-0, 2	0, 04
		-3, 2	10, 24		-0, 2	0, 04
б		1, 8	3, 24		-0, 2	0, 04
		2, 8	7, 84		0, 8	0, 64
		4, 8	23, 04		0, 8	0, 64
		2, 8	33, 64		0, 8	0, 64
		7, 8	60, 84		0, 8	0, 64
Итого			239, 60			5, 6

Таким образом, стаж продавцов отклоняется от среднего для первого магазина на 4, 9 года, а для второго магазина — 0, 75 года. Формула дисперсии для вариационного ряда с вариантами х и час­тотами/будет иметь вид:

где х — значение признака; 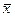— средняя арифметическая; f — частота.