
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уравнение Бернулли.
|
|
Зависимость давления идеальной жидкости от скорости ее стационарного течения и перепада высоты была установлена в математической форме Д. Бернулли в 1738 году.
Наиболее просто уравнение Бернулли можно вывести, если применить закон сохранения механической энергии к потоку жидкости. Для движения идеальной жидкости закон сохранения применим, т.к. в идеальной жидкости нет сил трения.
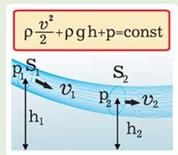
Пусть труба переменного сечения расположена наклонно к горизонту. Выделим некоторый объем жидкости между сечением АВ и сечением CD в узкой части (рис. 2.2.).
Пусть площадь поперечного сечения, давление и модуль скорости потока в широкой части соответственно равны S1, p1, v1, а в узкой части – S2, p2, v2.
Рис. 2.2.
Если жидкость течет слева направо, то под действием сил давления F1 и F2 и силы тяжести выделенный объем жидкости за малое время Dt сместится вправо и займет часть трубы, ограниченную сечениями А1В1 и C1D1. Силы давления F1 и F2 совершат работу
A = A1 + A2 = F1l1 – F2l2 = p1S1v1Dt – p2S2v2Dt.
Существенно, что при стационарном течении жидкости энергия объема жидкости, заключенного между сечениями S1 и S2 (рис 2.2.), остается неизменной. Все происходит так, как если бы жидкость, занимавшая объем АВВ1А1, переместилась бы и заняла объем СDD1C1. Поэтому достаточно учесть лишь изменение энергии элемента жидкости, переходящей из области АВВ1А1 в область СDD1C1. Работа внешних сил давления согласно закону сохранения энергии равна изменению энергии этого элемента. Его объем DV не изменяется вследствие несжимаемости жидкости.
Изменение энергии этого элемента жидкости равно:
DE = DEk + DEp= 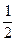 rDV(
rDV(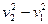 ) + rg(S2l2h2 – S1l1h1).
) + rg(S2l2h2 – S1l1h1).
Учитывая, что DЕ = А, получим:
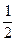 rDV(
rDV(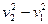 ) + rg(DVh2 - DVh1) = p1S1v1Dt - p2S2v2Dt.
) + rg(DVh2 - DVh1) = p1S1v1Dt - p2S2v2Dt.
Так как S1v1Dt = S2v2Dt = DV, то после сокращения на DV находим:
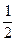 r
r 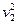 -
- 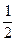 r
r 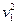 + rgh2 - rgh1 = p1 – p2.
+ rgh2 - rgh1 = p1 – p2.
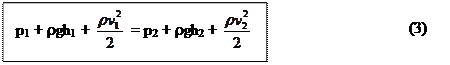 Откуда
Откуда
Это и есть уравнение Бернулли для течения идеальной жидкости.
Если труба горизонтальна, то h1 = h2 и уравнение принимает вид:
|
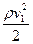 = p2 +
= p2 + 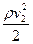 .
.
Уравнение (4) показывает, что с увеличением скорости течения (v 2 > v 1) давление в жидкости, текущей по горизонтальной трубе, уменьшается.