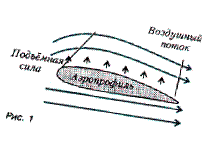
Теперь о подъемной силе крыла.

Классически возникновение подъемной силы объясняется тем, что, благодаря определенным очертаниям профиля крыла, скорость обтекания крыла воздухом сверху, больше, чем снизу. Причем, что заставляет двигаться воздух сверху быстрее, чем снизу? – Отвечают – непрерывность потока. Но вызывает большое сомнение корректность применения уравнения непрерывности не к несжимаемой жидкости в трубе, а к потоку легко сжимаемого воздуха в «свободном» пространстве. И как именно непрерывность приводит к увеличению скорости с одной стороны по сравнению с другой? Для природы в случае газовой среды нет некоего мистического «стремления к непрерывности», нужны конкретные физические причины изменения скорости. Они вовсе не очевидны. По закону Бернулли давление сверху за счет относительно большей скорости движения воздуха меньше, а снизу – больше. Но такое объяснение приводит к противоречиям с наблюдаемыми данными и теоретическим парадоксам. Перечислим некоторые из них еще раз:

- во-первых, (вопрос Дж. Раскина) как же тогда самолет может летать «вверх ногами»;

- во-вторых, по 3-ему закону Ньютона, испытывая действие подъемной силы со стороны набегающего потока, крыло само должно действовать на поток с противоположной по направлению и раной по модулю силой, что обязательно должно приводить к появлению у провзаимодействовавшего потока составляющей импульса, направленной вертикально вниз, что из закона Бернулли вовсе не следует;

- в-третьих, в случаях профилей крыла, предложенных в статье Дж. Раскина, скорость обтекания сверху выше, но эксперимент показывает (я его воспроизводил), что сила, действующая со стороны воздушного потока на крыло направлена вниз, а не вверх, как это следует из закона Бернулли;

- в-четвертых, воздушные змеи держатся в набегающем потоке без всякого особого профиля крыла, обеспечивающего «необходимую» разность скоростей обтекания, он просто «отбивает» часть набегающего потока вниз (точнее придает дополнительную вертикальную составляющую импульса);

- в-пятых, действие винта вертолета показывает, что воздух именно «отбивается» вниз, ведь у лопастей винта тот же профиль, что и укрыла.

Чтобы избежать этих противоречий и прийти к формуле подъемной силы, совпадающей с той, что приведена в Физическом энциклопедическом словаре (изд-во «Советская энциклопедия», Москва. 1983 год.) с точностью до некоторого коэффициента пропорциональности, предлагаем использовать просто 2-ой закон Ньютона. Рассуждения наши таковы: пусть налетающий на крыло воздушный поток приобретает после взаимодействия с ним добавочный импульс, направленный вниз. Грубо говоря, крыло должно для возникновения подъемной силы отбивать налетающие потоки воздуха вниз. Тогда и крыло будет по закону сохранения импульса получать импульс, направленный вверх. Так держатся в воздухе, например, воздушные змеи. Здесь особенно важна форма задней поверхности крыла, т.к. нужно, чтобы при отрыве от нее поток воздуха имел вертикальную составляющую импульса, направленную вниз. Даже если от него отрываются турбулентные вихри, то для существования подъемной силы крыла у этих вихрей кроме момента импульса, связанного с вращением, должна быть составляющая импульса центра масс, направленная вниз.

По второму закону Ньютона F = Δ P/ Δ t.

Оценим возможное изменение импульса Δ P, полученное налетающим потоком при взаимодействии с нижней частью крыла:

Δ P = v·Δ m,

Δ m = r Δ V,

Δ V = S ·Δ h,

Δ h = Δ l·sina;

=> Δ h = v·Δ t·sina => Δ V = S·v·Δ t·sina => Δ m = r· S·v·Δ t·sina=>

Δ l = v·Δ t, => Δ P = r· S·v²·Δ t·sina => F = Δ P/Δ t = r· S·v²·sina

где v – скорость налетания потока на крыло, S – площадь крыла, r - плотность налетающего потока воздуха вблизи крыла, Δ h – толщина слоя, соприкасающегося с крылом (см. рисунок).

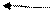
α

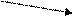dh

рис. 2.2.2.

Получаем, что подъемная сила будет пропорциональна

F ~ r S v ² sina,

при малых углах атаки a (а реальный угол атаки не более 5⁰ в горизонтальном полете и не более 10⁰ при взлете, при 15⁰ происходит переворачивание самолета), sina ® a, можно заменить на сам угол a. В энциклопедическом словаре на стр. 559 находим такую же формулу:

F = c_y r S v ² / 2,

где c_y = 2m (a - a₀),

а m – коэффициент, зависящий только от формы крыла,

(a - a₀) – это угол атаки, в нашей формуле просто a.

Как видим, форма крыла влияет на процесс через некий безразмерный коэффициент. Таким образом, о бе формулы при малых углах атаки отличаются лишь этим безразмерным коэффициентом, который определяется формой крыла! Это замечательное совпадение, говорит о том, что наш подход не противоречит наблюдаемым данным!

С нашей точки зрения главное требование в форме профиля крыла – это обтекаемость, иначе слишком велико будет аэродинамическое сопротивление крыла, а так же возникнет сильная область разряжения над крылом, куда будет затруднено попадание набегающего потока воздуха. Это, в свою очередь создаст различные турбулентности и выведет режим полета из состояния ламинарного обтекания, что может в лучшем случае привести к вибрациям (т.е. рывками будет изменяться угол наклона крыла и туда все же будут порциями поступать воздушные массы, так, например, летает воздушный змей, у которого нет обтекаемой формы), в худшем к переворачиванию крыла. Если хорошая обтекаемость обеспечена, то неважно с какой стороны профиль боле выпуклый, а с какой – более плоский. Главное – чтобы был угол атаки, отличный от нуля. И тогда, согласно нашим выводам будет возникать подъемная сила, позволяющая самолетам летать и прямо и «вверх ногами».

И вовсе не обязательно, чтобы скорость обтекания сверху и снизу была разной, т.е. закон Бернулли действует весьма косвенно. Иначе бы действительно самолеты не могли летать «вниз головой». У тех же дельтапланов из-за очень тонкой ткани никакой существенной разницы в длине пробега потока вдоль крыла вверху и внизу практически нет, а значит и скорости практически равны, а подъемная сила есть, а по закону Бернулли ее в таком случае не должно быть. Кстати, приведенный в данной статье словаря экспериментальный график зависимости c_y от a (c_y = c_y(a)) больше похож на участок синусоиды, чем на предлагаемую в статье прямую пропорциональную зависимость. Представленные же в статье Раскина в опытной установке (рис.9) крылья разного профиля (рис. 10) должны вести себя так: если при взаимодействии с крылом в момент отрыва струя воздуха приобретает дополнительный импульс, в одну сторону (а по форме профиля крыла можно догадаться, куда он будет направлен), то крыло будет двигаться в противоположную. Это, кстати, подтверждает его опыт с вогнутым профилем крыла.

Еще одно, смущавшее нас противоречие, попробуем ясно выразить: во многих пособиях указывается, что в системе отсчета, связанной с самолетом, вокруг крыла образуется круговое движение воздуха, т.е. часть воздуха приобретает момент количества движения. Возникает два вопроса: во-первых, откуда он берется, если по закону сохранения момента количества движения его возникнуть не должно, либо должны возникать еще вихри воздуха с противоположным моментом количества движения. Во-вторых, обычно после взаимодействия с крылом движение струй воздуха в этих пособиях изображается ламинарным, т.е. момент количества движения отсутствует. Однако, если момент количества движения есть в одной системе отсчета, то в другой – инерциальной по отношению к первой, связанной с воздухом, – он должен оставаться, т.е. движение воздуха после его взаимодействия с крылом самолета должно быть обязательно вихревым при любых углах атаки. Это в случае, если объяснять появление подъемной силы с привлечением закона Бернулли. Здесь как-то многое не вяжется и с наблюдениями за поведением струй воздуха, провзаимодействовавших с крылом, и с теорией рассмотрения данного вопроса. Результатом реактивного давления крыла на воздух (по третьему закону Ньютона - она есть ответная сила на подъемную силу) логично было бы считать его движение вниз, а не появление у него момента количества движения.

Есть еще один аспект, который аналогичен рассмотренной выше первой задаче о движении подкрученного мяча. Это аспект астрономический. Дело в том, что взаимодействие Земли с солнечным ветром носит очень похожий характер на взаимодействие подкрученного мяча с потоком воздуха. Только с учетом направления солнечного ветра – от Солнца к Земле, при ее вращении могут возникнуть эффекты замедления вращения Земли и замедления ее движения по орбите. Разумеется, эти эффекты очень слабы. Но если учесть, что они действуют миллиарды лет, то следствия могут быть ощутимы для движения Земли вокруг собственной оси и вокруг Солнца. Еще интересней станет ситуация, если данный подход применить к системе двойных звезд, где происходит активная аккреция газа с одной звезды – на другую. В этом случае данный эффект будет проявляться значительно сильнее. В одном случае это будет способствовать приближению одной звезды к другой, а в другом (в зависимости от направления вращения) – наоборот.

§ 2.4.

Заключение.

Человечество, начиная с 18-ого века, активно осваивает «пятый океан» - атмосферу Земли. Древняя мечта человечества – мечта о полете, наконец-то, осуществлена. Казалось бы, давно все хорошо изучено и освоено в таких областях как, воздухоплавание и аэродинамика. Построены и проектируются мощные и надежные летательные аппараты. Однако оказывается в этих областях не все так просто, как кажется на первый взгляд. Даже полет обычного футбольного мяча таит в себе парадоксы и загадки. К объяснению появления подъемной силы крыла, к ее расчету, как мы убедились, существуют различные подходы, причем дающие примерно одинаковые результаты в определенных случаях. Окончательный результат – какой же из этих подходов является правильным – может быть разрешен только в будущем с помощью экспериментов и уточнения теории. Мы тоже построили экспериментальную установку, которая поможет просветить правильный подход, проверить некоторые идеи. Установка эта представляет собой вариант крутильных весов, на которые закрепляются модели крыльев с различными профилями, а обдуваются они воздухом с помощью обычного вентилятора. Пока эта установка еще не доведена «до ума», она дает некоторые погрешности, но и дает обнадеживающие нас результаты. Мы собираемся усовершенствовать ее и методику проведения модельных экспериментов на ней. Так что, возможно, в недалеком будущем нам удастся получить окончательно верное толкование подъемной силы крыла и формулы для ее расчета.

Используемая литература.

1. Физический энциклопедический словарь. Изд-во «Советская энциклопедия», Москва, 1983 г. с. 559.

2. Дж. Раскин. «Окрыленный эффектом Коанда». Журнал «Квант» №5 1997 г. с. 6-10.

3. Мякишев Г. Я. «Молекулярная физика». Учебник для классов с углубленным изучением физики.

4. Стасенко А. Л. «Физика полета». Москва, «Наука» 1988г.