
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Эффект Коанда.
|
|
Однако данное толкование подъемной силы во многих случаях не является удовлетворительным. Существуют и другие подходы к решению данной задачи. В статье «Окрыленный эффектом Коанда», опубликованной в журнале «Квант» №3 за 1997 год ее автор, Джеф Раскин, профессор Калифорнийского университета в Сан-Диего, один из разработчиков компьютера «Macintosh» предлагает свои изыскания на тему подъемной силы, предварительно приводя несколько опытных фактов, которые могут поставить в тупик даже ученых, пользующихся общепринятым объяснением.
Итак, обратимся к материалам выше упомянутой статьи.
Читая введение в популярную книгу Д. Макоуля “Особенности работы технических устройств”, находим такую фразу: “Поперечное сечение крыла имеет форму, называемую аэродинамическим профилем. При движении воздух обтекает крыло. Профиль крыла искривлен так, что поток воздуха, обтекающий крыло сверху, движется быстрее, чем поток воздуха, обтекающий крыло снизу. Быстро движущийся воздух имеет более низкое давление, чем медленно движущийся. Поэтому давление воздуха под крылом более высоко, чем под ним. Эта разность давлений создает силу, которая вынуждает крыло подниматься вверх. Такую силу называют подъемной силой”.
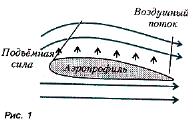
Данное рассуждение безоговорочно обращается к эффекту Бернулли, который устанавливает, что чем быстрее воздух движется вдоль некоторой поверхности тела, тем ниже его давление на эту поверхность.
Сегодня, когда большинство самолетных крыльев имеет значительно большую кривизну крыльев сверху, чем снизу, такому объяснению, казалось бы, можно поверить. Но тогда возникает вопрос: как же тогда самолет может летать верхом вниз?
Раскин выполнил расчеты на основе общепринятого объяснения работы крыла. Используя данные, полученные на моделях самолета, он нашел, что вычисленная подъемная сила составляет только 2% от силы, необходимой для полета модели. Здесь появляется второй вопрос: что же является основным источником подъемной силы, если не тот перепад давлений сверху и снизу крыла, о котором говорилось выше?
Традиционное объяснение работы крыла приводит нас к заключению, например, о том, что крыло, которое имеет слегка вогнутый низ,
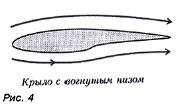
будет всегда испытывать, при прочих равных условиях, меньшую подъемную силу по сравнении с плоскодонным крылом. Ведь у вогнутого снизу крыла путь воздуха вдоль нижней части профиля длиннее чем у плоскодонного
Поэтому подъемная сила должна быть меньше. Однако на практике это не так.
Кроме того, как же плоское крыло, подобное тому, которое имеет бумажный планер, без каких бы то ни было искривлений, может обеспечить подъемную силу? Заметим, что плоское расположено под углом к направлению движения планера. Этот наклон называется “углом атаки” и является необходимым для создания подъемной силы плоского крыла. Позже мы вернемся к этой теме.
Формы поперечных сечений авиационных крыльев называются “аэродинамическими профилями”. Очень эффективным профилем крыла для небольших медленно летающих моделей является кусок какого-либо листового материала, изогнутый в виде арки. Однако из общепринятого объяснения вообще не ясно, как такое крыло, у которого верх и низ профиля имеют одинаковую длину может создавать хоть какую-нибудь подъемную силу. Если бы общепринятый взгляд был корректным, мы могли бы делать верх крыльев даже более криволинейным (изогнутым) по сравнению с тем, как его делают сегодня. В этом случае воздух двигался бы еще быстрее, и мы получили бы еще большую подъемную силу. Но в действительности же такое волнообразное крыло может привести к катастрофе.

Итак, несмотря на то, что уравнение Бернулли является правильным, его применение к решению вопросов об аэродинамической подъемной силе вносит значительную путаницу в выводы, основанные на использовании общепринятых представлений. Правильно примененное или нет, это уравнение предлагает не очень удобный образ того, что связывает форму профиля крыла с его подъемной силой, и ничего не говорит о силе вязкого трения. Эта трудность, объединенная с повсеместным существованием правдоподобно звучащего общепринятого мнения, вероятно, объясняет, почему даже некоторые превосходные физики были введены в заблуждение.
Если это аргумент, что профили крыльев создают подъемную силу исключительно потому, что поток воздуха у поверхности понижает давление на эту поверхность. То при искривлении поверхности не имеет значения, является ли она прямой, вогнутой или выпуклой. Общепринятое объяснение дает зависимость только от скорости потока, параллельного поверхности. Здесь предлагается рассмотреть несколько опытов, которые можно легко воспроизвести для проверки этого утверждения.
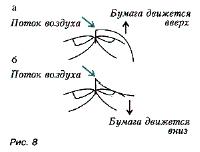
Опыт 1 Возьмем полосу писчей бумаги размером 5 х 25 см. Если держать ее перед губами так, чтобы она высовывалась из пальцев и обвисала, делая верхнюю поверхность выпуклой, то когда вы подуете поверх бумаги, она поднимется. Много книг объясняют этот эффект понижением давления воздуха сверху из-за действия эффекта Бернулли. Затем придадим бумаге форму кривой так, чтобы ее верхняя поверхность стала слегка вогнутой вдоль всей длины, и вновь подуем поверх полоски. Теперь бумага будет двигаться вниз.
Опыт 2. Здесь предлагается с помощью пылесоса сделать своеобразную модель аэродинамической трубы с помещенным внутри крылом, удерживаемым при помощи пары осей, которые позволяют ему свободно поворачиваться вверх и вниз. Воздух подается помощью пылесоса.
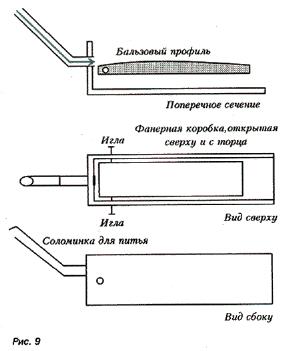
Когда воздух начинает продуваться через трубу, крыло со стандартным профилем (рис.9.) вверху и плоское снизу немедленно отрывается от дна и поднимается. Когда продувка прекращается крыло снова «падает» вниз. Это и есть то, что все ожидают.
Теперь рассмотрим крыло, у которого форма кривой та же самая, но образуемая поверхность уже вогнутая, т.е. обращена выпуклостью вниз. Если бы общепринятое объяснение было бы верно, то следует ожидать, что это крыло тоже поднимется, ведь профиль и длина кривой те же. И в этом случае воздушный поток вдоль поверхности должен иметь пониженное давление, приводящее к появлению подъемной силы. Однако вогнутое крыло останется внизу. Если же крыло поставить вертикально, то можно увидеть, что крыло будет отклоняться прочь от воздушного потока.

Таким образом, часто цитируемый опыт, который обычно используется, как демонстрация общепринятого объяснения подъемной силы не может быть объяснен только действием эффекта Бернулли. Какой то другой эффект оказывается гораздо сильнее. Для изображенных профилей мы провели собственные эксперименты, результаты которых будут приведены ниже.
Еще один парадокс – вращающийся мяч.
Траектория мяча, движущегося в воздухе поступательно в горизонтальной плоскости и при этом вращающегося вокруг своей вертикальной оси, отклоняется влево или вправо (в зависимости от направления закрутки) от первоначально заданного направления. Опыт показал, что этот эффект зависит, во-первых, от степени закрученности мяча (скорости его вращения), и во-вторых от наличия среды (воздуха). Незакрученные мячи или закрученные в вакууме движутся по прямой.
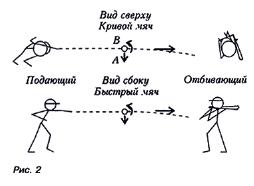
Из-за шероховатости поверхности мяча действие вязких сил приводит к возникновению тонкого слоя воздуха, вращающегося вместе с этой поверхностью. Рассматривая рисунок, можно понять, что скорость набегающего воздуха в точке, обозначенной буквой А, будет выше, чем скорость воздуха в точке В. Происходит это потому, что в первом случае скорость вращательного движения точек поверхности мяча и увлекаемого им тонкого слоя воздуха складывается со скоростью набегающего воздушного потока, а во втором захваченный мячом воздух будет тормозить встречный воздушный поток, уменьшая его скорость. Разность давлений со стороны этих потоков вызовет появление силы отклоняющей мяч в сторону направления его вращения.
Наиболее наглядно это можно наблюдать если использовать для опыта пляжный легкий пластмассовый мяч. Закрученный вокруг своей горизонтальной оси так, чтобы его нижняя часть вращалась по направлению его движения, мяч пока скорость его поступательного движения будет достаточной, поднимается вверх и лишь затем под действием силы тяжести падает. Это же явление используется в футболе, когда мяч после удара движется по дуге в сторону направления его вращения (удар известный под названием «сухой лист»).
Надо сказать, что существуют и другие объяснения упомянутого эффекта, которые связывают его, например, с турбулентными вихрями, трением и несколько иным толкованием эффекта Бернулли. Но приведенное объяснение кажется автору правильным.
Джеф Раскин предлагает свое объяснение приведенных выше парадоксов. Это объяснение основывается на т.н. эффекте Коанда. Заключается этот эффект в следующем. Если струя воды течет вдоль поверхности твердого тела. Которая слегка искривлена в сторону струи, вода имеет тенденцию следовать этой поверхности. Это одно из проявлений эффекта Коанда. Которое легко демонстрируется, например с помощью ложки и тонкой струйки воды из водопроводного крана. Если держать ложку так, чтобы она могла качаться, и приблизить ее к струе, то можно почувствовать, как ложка дернется по направлению к потоку воды. Это – проявление третьего закона Ньютона: если ложка притягивает воду, то и струя должна притягивать ложку.
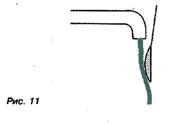
Эффект имеет границы. Если вы используете сферу вместо ложки, то обнаружите, что вода будет следовать только части пути. К тому же, если поверхность резко искривлена, вода не будет следовать ей, а будет только немного изгибаться и сразу же отрываться от поверхности. Джеф Раскин считает, что именно эффект Коанда помогает нам понять, почему угол атаки (крыла с равным наклоном во всю длину) является решающе важным; почему самолеты могут летать перевернутыми; почему «действуют» плоские и тонкие крылья и т.п.
Однако эффект Коанда очень слаб, а потому вряд ли можно согласиться с Раскиным в этой части его рассуждений о роли этого эффекта в образовании подъемной силы крыла и других аэродинамических эффектов. Но сами парадоксы, отмечены им очень цепко и остроумно. Тут есть над чем поразмышлять критически настроенному трезвому уму.
§ 3.