ВОПРОС 6. Верификация линей. мод.. Коэфф. детерминации. Значимость модели.

После оценив. пар-ов мод. необх. исслед., насколько постр-ая мод. опис-ет изуч-е завис.. Если окажется, что расхож. между получ. мод. и эмпирич. данными, либо между мод. и экономич. знаниями об изуч. зависим. велики, предстоит коррект. или перестройка мод.. Прич., обуславл. низкое кач-во эконометрич. мод. могут прояв. уже на начал. этапах эконометрич. иссл-я. Нельзя быть уверен., правил. ли подобр. объ-щие пер-ые. Сомнения мож. вызывать выб-ая аналит. форма мод.. В проц. оценки структур. пар-ов мод. может примен. некоррек. метод оценив.. Всё это делает необход..провер. построен. мод. до нач. её использ. для формул-я выводов об иссл-ых зависим..Верифик. мод. свод. к изуч.3-х хар-к: 1.степени соотв. мод. эмпирич. данным; 2.кач-ва оцен. структур. пар-ов; 3.распредел. случ. отклон..

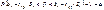
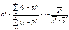
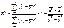Оцен. соотв. модели эмпир. данным имеет целью устан., в достат. ли степ. эта модель отобр. формир-е объ-мой пер-ой. Для этого использ. различ. меры согл. мод. с эмпирич. данными. Одной из основных мер счит. коэфф. детерм. для нелин. мод.и и для линейной модели.

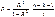Его знач. лежат в пром. [0, 1]. Он показ. какая доля полной вариации объ-мой пер-ой определ. её теоретич. хар-ми, т.е. детермин. объ-ми пер-ми. Мод. тем лучше адаптир. к данным, чем ближе к 1 знач. коэфф. детерм. В случае линей. мод. квадрат.корень из коэфф. детерм., то есть R, представ. собой коэфф. множест. корр.. Для того чтобы пров., достаточно ли высока степень адапт. мод. к эмпир. данным, нужно пров. гипот.о знач. коэфф. множеств. корр., т.е. H0: [R=0] и H1: [R не =0]. Пров. гипот. счит. стат. Эта стат. имеет F -распред. Фишера-Снедекора с m1=k и m2=n-k-1 степ. своб. 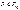Из табл/ F -теста для задан. уровня знач. альфа и m1, m2 степ. своб. выб. крит. знач. F кр. Если F< или =Fкр, то гип H0. Это означ, что коэфф. множест. корр. несущ. отлич. от нуля, следов., мод. слишком слабо адапт. к эмпир. данным. Если F> Fкр, то гипот. H1.