ВОПРОС 9. Исследование св-в случ. откл.. Исследование нормальности распределения.

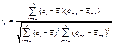
Случ. откл. должны иметь нормал. распред., гомоскедастичны, не автокорр., а также в случ. откл. не должна присутст. зависимость, т.е. они д.б. случайны. Исслед. нормальности распред. случ. откл. сводится к вериф. гип. о том, что фу-я распред. откл. F(e) явл. фу-ей норм. распред. FN(e). Итак, гип. H0: [F(e)= FN(e)] и Н1. Для вериф. гип. о нормальн. распред. прим. тест Хельвига. Алгоритм. 1.Проводится стандартизация остат. по ф-ле

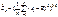где - е (с палкой верху) сред. ариф. остат. еt, - стандартноеоткл. остат. еt., расс. по ф-ле

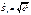
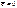в случае линей. мод. и стандарт. откл. равно

2.Стандартизов. ост. упоряд. по возрас.:.

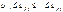3. Из табл. ф-ии нормал. распред. выб. знач. ф-ии.

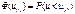4. Опред-ются цели It, в роли к-х высту. числ-ые интерв. шир. 1/n, образ-ые делением отрезка [0, 1] на n равных частей. 5.Знач. ф-ии Ф(U(i)) припис. соотв. целям, потом опред. кол-во пустых целей, в к-ые не попало ни 1 знач. Ф(U(i)). 6. Из табл. теста согл. Хельвига для данн. кол-ва наблю. n и для прин. ур. знач. альфа выбир. крит. знач. k1 и k2. 7. Если k1< или равно k< или равно k2, то гип. H0. Случ. откл. в этом случае носят норм. хар-р. Если k< k1 или k> k2, то гип. H1, т.е. случ. откл.не имеют норм. хар-ра, оценки пар-ов мод. треб. уточнения.

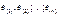Для пров. норм-сти распред. остат. мод. можно использ. тест Шапиро-Вилька. Алгоритм.Остат. упорядоч. по возрас. до получ. последоват..

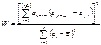8.Рассч. знач. стат.

где [n/2] - целая часть числа n/2; 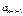- коэфф. Шапиро-Вилька, опред. по табл.; в случае линей. мод. .

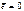9.Из табл. теста Ш-В для прин. уров.знач. альфа выбир. крит. знач.Wкр. 10. Если W> не равно Wкр, то гип. Н0. В против. случае, приним. гип. Н1, т.е. остат. не имеют норм. распред., оценки пар-в мод. треб. уточнения.

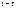
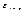ВОПРОС 10. Исслед. св-в случ.откл.. Исслед. автокорр. Автокорр. случ. откл. говорит. о линей. зависим. между этими откл., произошед. в различ. момен. врем.. Мерой силы и направл. автокорр. случ. откл. Et в период t и случ. откл. в период служит коэфф. корр.

,

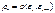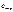
наз. коэфф. автокорр. порядка. В кач. оценки этого коэфф.расс.коэфф. автокорр. остат. et и, рассч. по ф-ле

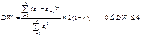Для вериф. гип. об отсут. автокорр. 1-го порядка, т.е. гип. Н0: [p1=0] либо H1: [p1> 0] либо H2: [p2< 0] прим/ тест Дарбина-Уотсона. Для пров. нулевой гип. расс. стат. Д-У

.

Из табл. теста Д-У для прин. уровня знач. альфа и задан. кол-ва наблюд. n при кол-ве объ-щих пер-ых k выб. 2 кр. знач. 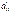и 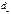. По этим знач. отрезок [0, 4] разбив. на 5 зон. В зависим. от того, в какую зону попадает расч. знач. крит., прин. или отвер. соотв. гип.

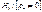
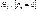Наличие зоны неопределенности связано с тем, что распред. DW –статис. зависит не только от числа наблюд. и числа объ-щих пер-ых, но и от знач.объ-щих пер-х. Существенность отриц. автокорр. случ. откл. произвольной последоват. может исследоваться с помощью теста существенности коэфф. корр.. Этот тест позволяет вериф. гип.. Критерием этой гип. служит статис.

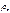
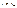
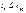
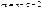
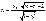Из таблицы t -теста Стъюдента для прин. уровня знач. альфа и для степ. своб. выб. крит. знач. t кр. Если, то гип. Н0, т. е. коэфф. автокорр. несуществ. Если то гип. Н1, т.е. коэфф. автокорр. существ., в остатках мод. присутствует автокорр., необх. уточнить оценки пар-ов мод..