ВОПРОС 11. Исследование св-в случ. откл.. Исследование стабильности дисперсии.

Одним из усл. адекват. мод. явл. предполож. о постоянстве диспер. случ. члена для всех наблюдений (гомоскедастичность). Если это условие не соблюдается, то имеет место гетероскедастичность. Если наблюд. гетероскед. случ. откл., то МНК-оценки будут неэффектив., занижен., следовательно, t-статис. будет завышена. Это может привести к статис. знач. коэфф., тогда как в действител. это неверно.

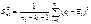
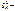
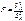Одним из способ. исслед. стабильности диспер. случ. откл. считается пров. гип. о равенстве дисперсий 2х крайних групп наблюд. знач. Для вериф. гип. о равенстве дисперсий случ. откл. этих подмножеств использ. F -тест. Крит. этой гип. служит статис. где остаточная дисперсия n1 первых наблюдений:

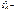остаточная дисперсия n2 последних наблюд:

.

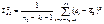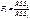Из табл. F -теста для прин. уровня знач. альфа и для m1=n2-k-1 и m2=n1-k-1 степ. своб. выб. крит. знач. стат. Fкр. Если F< или = Fкр, то гип. Н0, дисперсия случ. откл. стабильна во времени. Если же F> Fкр, то гип. Н1 дисп. случ. откл. возрастает, необх. уточ. оценки пар-ов мод. Для пров. гомоскедастичности могут также примен. др. тесты. Тест Голдфельда-Квандта (прим. в предпол., что стандарт. откл. случ. члена пропорцион. знач. независ. пер-ой X). Алгоритм.1. Все n наблюд. в выборке упорядоч. по возраст. пер-ой X.2. Оцен-тся отдел. регресс. для 1-х n0 и для посл-х n0 наблюд. 3. Состав. статис.

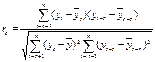
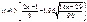
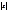где RSS1 и RSS2 - суммы квадратов остатков для 1-х и последних n0 наблюд. соответ. По табл. для прин. уровня знач. альфа и для m1=n0-k-1 степ. своб. выб. крит. знач. статис. Fкр. Если F< или =Fкр, то гип. H0, т.е. диспер. случ. откл. стабильна во времени. Если F> Fкр, то гип. Н1, т.е. диспер. случ. откл. возрас., необх. уточнить оценки пар-ов мод. Тест ранговой корр. Спирмена.Алгоритм. 1.Выдвиг. нулевая гип. об отсут. гетероскедас. случ. откл.2. Данные по x и остатки ранжируются по пер-й x и опред. их ранги. Ранг – это поряд. номер знач. пер-й в ранжирован. ряду.3. Опред. коэфф. ранговой корр. Спирмена по фоp-е,

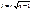
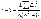где Di – разнос. меж. ранг. x и 4. Состав. статис., к-ая срав. с tкр для задан. уровня знач. (tкр=1, 96 при альфа=0, 05 и tкр=2, 58 при альфа=0, 01).Если t> tкр, то нулевая гип. об отсут. гетероскедас. откл.

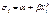
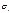Тест Глейзера. Используя абсолютные знач. остат. в кач-ве оценки оценивается регрессия при различных знач. Выб. наилуч. оценка (с наибольш. знач. коэфф. детермин.) и пров. знач. пар-ра бетта. В случае, если коэфф. бета значим, то нулевая гип. об отсутст. гетероскедас.откл.