
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Описание модели города на окружности.
|
|
Еще одним вариантом модели пространственной дифференциации рынка является модель города на окружности Сэлопа. Прообразом этой модели является город, вытянувшийся вдоль берега острова, имеющего округлую форму, либо же город, в котором все супермаркеты вынесены на периферию и расположены вдоль внешнего кольцевого хайвэя. Как писал сам Сэлоп, его модель является вариацией более ранней модели Хотелинга, модели линейного города.
Впервые свою модель Сэлоп описал в журнале «The Bell Journal of Economics. Volume 10, №1», выпущенном весной 1979 года. Эта модель позволяет рассмотреть вопросы дифференциации при большом количестве фирм, действующих на рынке, а также при отсутствии барьеров входа, кроме входных затрат.
Рассмотрим город, вытянувшийся на окружности единичной протяженности (2pP = 1), вдоль которой, на равном расстоянии друг от друга,
размещаются N торговых точек. Также вдоль окружности равномерно, сединичной плотностью размещено население города L. Перемещения покупателя j происходят также по окружности, каждое перемещение обходятся ему в t денежных единиц за единицу расстояния. Графическая модель такого города представлена на рис. 3.1, где местоположение торговых точек показано красными квадратами, а нахождение покупателей синими.
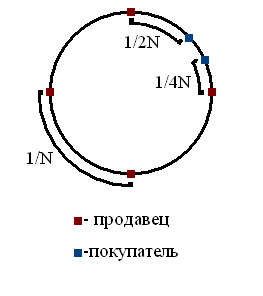
Рис 3.1 Графическое представление модели города на окружности.
При любомколичестве магазинов, расстояние между двумя лавками составит 1/N. Так как население размещено на окружности с одинаковой плотностью и равноудалено друг от друга, то ни один из покупателей не будет находится от ближайшего к нему магазина более чем на расстояние равное 1/2N, так что среднее расстояние, которое придется преодолевать покупателю до ближайшего магазина, составит 1/4N и, следовательно, расстояние до магазина и обратно в среднем составит 1/2N. Каждый покупатель посещает магазин один раз в день в день. Каждый продавец имеет функцию затрат:
С= F + cQ
где С = Т С (общие издержки)
F = ТFС (общие постоянные издержки)
с =МС (предельные затраты)
Следовательно, его средние затраты выражаются следующим уравнением:
АТС =F/Q + с
Считается, что чем большее число покупателей обслуживает магазин, а
следовательно чем больше он реализует продукции, тем ниже его средние затраты.Транспортные расходы можно представить как убывающую функцию количества магазинов, так как с ростом числа магазинов расстояние между нами сокращается. При тарифе t за единицу пути общие транспортные расходы, Сt, будут равны произведению численности домохозяйств на среднюю стоимость поездки в магазин и обратно:
Сt = tN/2N (1)
Общие расходы на покупку товаров, Сg, также зависят от числа магазинов и домохозяйств:
Сg = Lc + NF (2)
где Lc - общая сумма предельных затрат, оплачиваемых покупателями.
NF - общие постоянные затраты всех магазинов.
Чтобы определить оптимальное количество магазинов, необходимо минимизировать сумму общих транспортных расходов и общих расходов на покупку товаров:
С = Сt + Сg
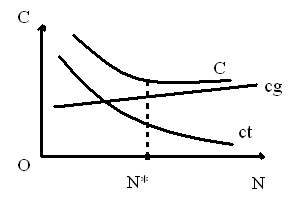
Рис.3.2 Рыночный оптимум
Обе функции затрат, (1) и (2), показаны на рис. 3.2, где N* минимизирующее С (издержки) число магазинов. При таком их количестве наклон кривой Сg по своей абсолютной величине равен наклону кривой Сt. Таким образом, оптимальное число магазинов должно удовлетворять условию:
tL/2(N*)2 = F (3)
откуда:
N* = √ (tL/2F) (4)
Заметим, что наклон кривой Сt характеризует общую экономию транспортных расходов при малом увеличении N.
Рисунок 3.3 а демонстрирует ситуацию, когда О устанавливает цену выше чем у своих конкурентов, тогда как на рисунке 3.3 б, О устанавливает цену ниже чем его «соседи».

Рис.3.3 Линейная часть города на окружности.
(Гальперин В. М., Игнатьев С. М., Моргунов В. И.
Микроэкономика
II том. Институт " Экономическая школа", Санкт-Петербург, 2004
Глава 12, пункт 7)
Рассмотрим спрос на услуги лавки. Он будет зависеть от соотношения установленных продавцом цен и цен его конкурентов. Рис. 3.3 показывает (для простоты) фрагмент города, лежащего на окружности, в центре расположен магазин О, а с лева и с праваего ближайшие конкурентфы, слева (-1/ N) и справа (+1/ N). Допустим, что магазин Оустанавливает цену PO, тогда оба его соседа придерживаются более низкой цены.
Для потребителя, живущего на расстоянии l от магазина О, стоимость покупки в этом магазине, включая затраты на поездку, составит:
СO(PO) = PO+2tl (3)
Для покупателя, живущего рядом с магазином О, который не имеет транспортнх издержек, стоимость покупки в этом магазине равна цене товара:
СO(PO) = PO
На рисунке 3.3, две линии, исходящие из PO влево и вправо, характеризуют общую стоимость покупки товара в магазине О как функцию цены товара и местоположения потребителя.
Определим общую стоимость покупки товара потребителем в магазине, расположенном в точке + 1/N. Представим расстояние, определяющее его местожительство от этого магазина, в виде разности +1/N - l. Тогда его общие затраты на покупку товара в этом магазине составят:
C1(Р+1) = Р+1 + 2t(1/N - l) (4)
Линия, исходящая из Р +1 влево, характеризует общую стоимость покупки в этом магазине как функцию цены товара и местоположения покупателя. Поскольку Р -1 = Р +1, общая стоимость покупки товара, расположенного в точке -1/ N, аналогична (4).
Точки пересечения линий, отображающих общие затраты потребителей на покупку товара в двух близлежащих магазинах, характеризуют местоположение покупателя, для которого стоимость покупки в том и другом магазине одинакова, т. е. безразличного к выбору одного из двух мест покупки. Поскольку Р -1 = Р +1, эти точки расположены ближе к магазину О, чем к магазинам -1/ N и +1/ N. Понятно, что живущим на полпути (1/2N) от магазина О вправо и влево дешевле пользоваться услугами магазина О, чем его
конкурентов. Если бы цены конкурентов были ниже, чем в магазине О (Р - 1 = Р +1 < РO), точки пересечения линий общих затрат покупателей лежали бы ближе к местоположению магазина О, чем его конкурентов (рис. 3.3 б).
Теперь, когда нам известны точки безразличия покупателей в отношении выбора магазинов, мы можем определить численность клиентов каждого из этих магазинов, или «границы клеточек рынка» по Войтинскому, при данном уровне цен. Если магазин, размещенный в точке О, установит цену РO, а его конкурент справа цену Р +1, точку безразличия покупателей между этими магазинами (X +1) можно, как следует из рис. 3.3, определить, решив уравнение:
PO + 2tX+1 = Р+1 + 2t(1/N - X+1) (5)
Из (5) имеем X+1 = 1/4t(Р+1 - РO + 2t/N) (6)
Отметим, что, при Р+1 = РO
X+1 = 1/2N (7)
это соответствует половине расстояния между двумя магазинами.
Поскольку магазин О хотел бы привлечь покупателей и справа и слева от себя, общая длина дуги X -1 X +! будет вдвое превышать расстояние от точки О до точки X +1 (6). Поскольку общая численность домохозяйств города, L, равномерно распределена по окружности, мы можем определить клиентуру магазина О как:
Q = L/2N(Р+1 - РO + 2t/N) (8)
Мы можем представить это выражение (8) как функцию спроса на услуги магазина О, заметив, что с увеличением положительной разницы цен (Р +1 - РO) клиентура магазина О будет возрастать. Тогда обратной функцией спроса на услуги магазина О будет:
РO = (Р+1 + 2t/N) √ 2t/LQ (9)
Линейная функция спроса (9) позволяет определить функцию предельной выручки, которая имеет общую с ней точку на ординате и вдвое более крутой наклон:
MRO = Р+1 + 2t/i< > - 4t/LQ (10)
и предельной выручки магазина О, а также его прибылемаксимизирующие цена и объем продаж:
Р*O = (Р +1 + 2 y / N + c), (11)
Q*O = L /2 N + L /4 N (Р +1 - c) (12)
Из (10) следует, что Р*O возрастает с ростом Р+1, цены, Устанавливаемой соседним магазином, а также с увеличением транспортного тарифа t. Чем выше транспортные тарифы, тем более высокую цену может назначить магазин, поскольку покупатели, преодолевшие значительное расстояние, становятся для него более «ценными». Заметим, что прибылемаксимизирующая цена зависит также от предельных затрат с. Из (12) следует, что прибылемаксимизирующее Количество продаж, Q*O, возрастает с увеличением цены конкурента и сокращается с ростом транспортных расходов покупателей.
Формулы (11) и (12) можно упростить, предположив что все магазины имеют одинаковые предельные затраты и равный доступ на рынок. Тогда прибылемаксимизирующие цена и количество продаж окажутся одинаковыми для всех магазинов города. Заменив в (11) Р +! на Р* получим:
P* = 2t/N + c (13)
и, подставив (9) в (8), получим
Q* = L/N (14 )
Таким образом, если цены всех магазинов будут одинаковы, точки безразличия покупателей в отношении этих магазинов будут равномерно распределены по окружности и на долю каждого магазина придется часть рынка равная l/N. Наконец, экономическая прибыль каждого магазина составит в этом случае
p = P8Q* - F √ cQ* = (2 t / N + c)(L / N) - F - c (LN) = 2 tL / N 2 – F (15)
Здесь прибыль может оказаться положительной или отрицательной в зависимости от значений L, t, N и F.
Допустим, что экономическая прибыль (15) положительна. Приведет ли тогда
свободный вход в отрасль новых конкурентов к падению прибыли до нуля? Как это имеет место в моделях совершенной конкуренции и монополистической конкуренции Чемберлина. Абсолютно точного ответа на этот вопрос не существует. Решающее значение здесь имеет различие постоянных и безвозвратных затрат. Постоянными затратами мы называем затраты, не зависящие от объема выпуска, а поглощенные затраты (невозвратные) (англ. sunk costs) это окончательно совершенные затраты, которые никогда не смогут быть возвращены, даже если предприятие покинет отрасль. Поэтому они не являются альтернативными затратами. Примером безвозвратных затрат могут послужить расходы теплоэлектростанции на сооружение всех необходимых подземных коммуникаций.
Независимо от времени вступления на рынок магазин размещенный в точке 1/ N, не может изменить местоположение без потери затрат, вложенных в его размещение в данной точке рынка. Поэтому постоянные затраты F являются для уже существующего магазина невозвратными. Где же может тогда разместиться с наибольшей для себя выгодой новый (N +1)- й магазин,
если все l/N-е участки уже заняты N магазинами? Наилучшим вариантом для размещения нового магазина является размещение его на полпути между парой соседних уже действующих магазинов. Тогда его клиентура составит половину клиентуры соседних магазинов, а при неизменной цене Р*, его выручка и прибыль также оказались бы вдвое меньше, чем у них. Если бы появление нового продавца привело бы к некоторому снижению цены Р*, что более вероятно, его выручка и прибыль были бы, естественно, несколько ниже. С другой стороны, поскольку затраты (из-за наличия постоянной компоненты F) не снижаются пропорционально выпуску, возможно, что новичок не получит положительной экономической прибыли, тогда как укоренившиеся на рынке магазины будут рентабельны.
Принципиальное отличие пространственной модели монополистической конкуренции от модели Чемберлина заключается в том, что в модели Чемберлина любая фирма, в том числе и новичок, получает пропорциональную долю рыночного спроса и в итоге прибыль любой лавки в длительном периоде сводится к нулю. С другой стороны, в модели пространственной конкуренции с фиксированным местоположением уже функционирующих продавцов возможности новичка гораздо ниже возможностей уже устоявшихся на этом рынке продавцов. В этой модели совершенная свобода входа на рынок совмещается с наличием положительной экономической прибыли в длительном периоде. Однако это различие не абсолютно, так как предполагается, что
местоположение действующих торговцев фиксировано и одна фирма не может быть представлена несколькими филиалами. Но, логично предположить, что фирмы вольны выбирать свое местоположение, и при этом не нести колоссальных невозвратных затрат. На таком рынке возможности получения прибыли новичком ничуть не меньше, чем у ранее закрепившихся на нем торговцев. Таким образом, на этом рынке, как и в модели монополистической конкуренции Чемберлина, свобода входа приведет в длительном периоде к нулевой экономической прибыли для всех продавцов. Отсюда понятно, почему владельцы магазинов с фиксированным местоположением стремятся к колонизации чужих клеточек рынка, открывая свои филиалы на значительном расстоянии от места положения своих старых филиалов. Справедливость данного аспекта модели пространственной дифференциации подтверждается тем, что представители крупных торговых сетей, имеющие своих протеже в кругах власти, стремятся уменьшить количество мелких конкурентов, ради уменьшения эластичности спроса по цене, что в свою очередь ведет к увеличению монополистической власти конкурента на определенной
территории. Примером моих суждений могут послужить массовые сносы частных магазинчиков в большинстве крупных городов России, в частности в городе Красноярске только в течение 2014 года было снесено более одной тысячи ларьков.
Наконец, в нашей пространственной модели монополистической конкуренции экономическая прибыль в длительном периоде может оказаться положительной или нулевой. Чтобы определить оптимальное количество магазинов в этой ситуации, подставим в формулу (15) цену равную нулю p = 0. Тогда мы получим:
N** = √ (2tL/N) (16)
Сравним оптимальное в длительном периоде количество магазинов (16) с тем, что было определено ранее в формуле (4). Увидим, что N* вдвое меньше N**
√ (2tL/N)/√ (tL/2F) = √ 4 = 2 (17)
Иначе говоря, в последнем случае мы имеем избыточное разнообразие продуктов.
Надо, однако, иметь в виду, что этот вывод об избыточном разнообразии основан на статичном представлении действительности, когда предприятия решают, сколько заведомо известных товаров предлагать им на рынке. В действительности же новые вариации товаров обычно являются результатом исследований и разработок. Вполне вероятно, что, если число различных модификаций холодильников или компьютеров будет определено раз и навсегда, мы выиграем при их небольшом количестве. Однако процесс, способствующий росту разнообразия товаров, является следствием
многочисленных технологических нововведений, которые могут использоваться не только в производстве новых вариаций определенного блага, но и в производстве всей массы продуктов. Результаты этих нововведений должны поэтому учитываться для более полного сопоставления оптимального и равновесного разнообразия товарного мира.