
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Прогрессии
|
|
ЧИСЛА, ДРОБИ, МОДУЛИ
Множества:
Æ - пустое множество
N = {1, 2, 3, …} - множество натуральных чисел 
Z =  - множество целых чисел
- множество целых чисел
Q = 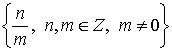 - множество рациональных чисел (дробей)
- множество рациональных чисел (дробей)
R – множество вещественных (действительных) чисел
Арифметические операции с дробями:
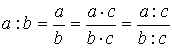 ,
, 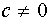 ;
; 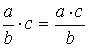 ;
; 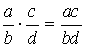 ;
; 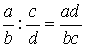 ;
; 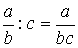 ;
; 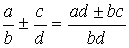 ;
;
Пропорция: 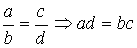 ;
;
Модуль числа:
Определение: 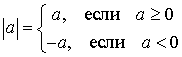 ;
;
Свойства модуля:
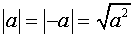 ;
; 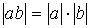 ;
; 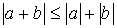 ;
; 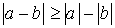 ;
; 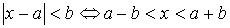
 ;
;

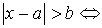
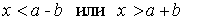
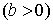 ;
;
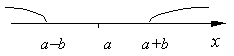
ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
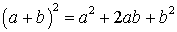 ;
;
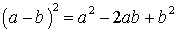 ;
;
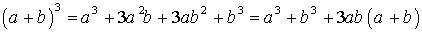 ;
;
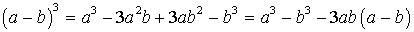 ;
;
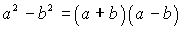 ;
;
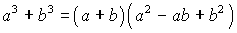 ;
;
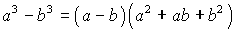 ;
;
СТЕПЕНИ И КОРНИ
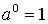 ;
; 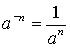 ;
; 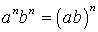 ;
; 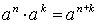 ;
; 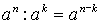 ;
; 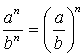 ;
; 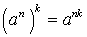 ;
; 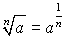 ;
; 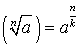 ;
; 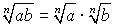 ;
; 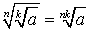 ;
;
Показательные неравенства:
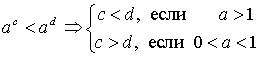 .
.
КВАДРАТНЫЕ УРАВНЕНИЯ
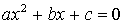 ;
; 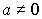 .
.
Корни уравнения: 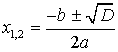 , где
, где 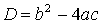 - дискриминант.
- дискриминант.
Формулы Виета: 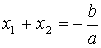 ;
; 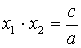 ,
,
где x 1 и x 2 – корни квадратного уравнения.
Разложение квадратного трехчлена на множители:
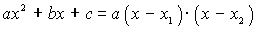 .
.
Приведенное уравнение: 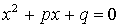 ;
; 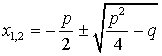 .
.
Квадратное неравенство:
если D > 0, a > 0, 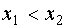 , то
, то
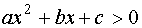
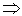
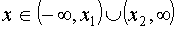 - “решение за корнями”
- “решение за корнями”
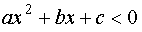
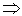
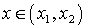 - “решение между корнями”,
- “решение между корнями”,
где 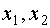 - корни квадратного трехчлена.
- корни квадратного трехчлена.
ПРОГРЕССИИ
Арифметическая прогрессия: 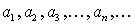
Общий член: 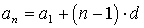 ,
, 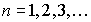 , где
, где 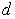 - разность прогрессии;
- разность прогрессии;
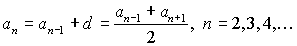
Частичная сумма: 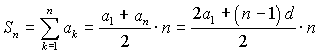 .
.
Геометрическая прогрессия: 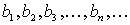
Общий член: 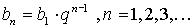 , где
, где 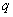 - знаменатель прогрессии;
- знаменатель прогрессии;
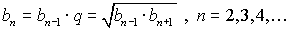
Частичная сумма: 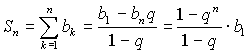 .
.
Сумма бесконечно-убывающей геометрической прогрессии (при 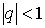 ):
): 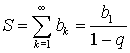 .
.
Некоторые суммы:
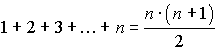 ;
; 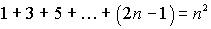 ;
;
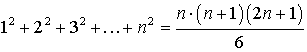 ;
;
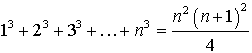 ;
; 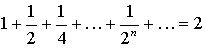 ;
;