Окружность и круг.

Длина окружности: ;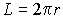

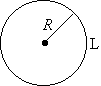
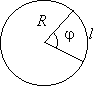
длина дуги окружности:

; ;

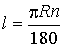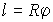(n - величина дуги в градусах, j - величина дуги в радианах).

Площадь круга: ;

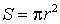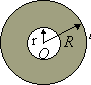
площадь кольца: ;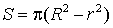

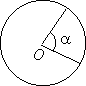площадь сектора: ,

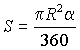где a - величина дуги в градусах.

Свойства окружности:

1) касательная и радиус, проведенный в точку касания,

перпендикулярны: r ^ l.

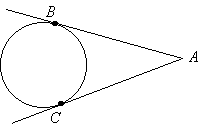2) отрезки касательных, проведенные

к окружности из точки, лежащей вне ее,

равны: AB = AC

3) диаметр, перпендикулярный хорде,

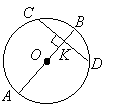делит ее пополам;

диаметр, проходящий через середину хорды,

перпендикулярен ей:

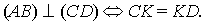
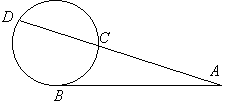4) квадрат длины касательной равен

произведению длины секущей

на ее внешнюю часть:

AB ² = .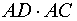

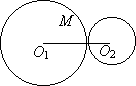5) центры касающихся окружностей О ₁, О ₂

и точка их касания М лежат на одной прямой.

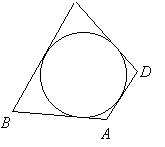6) в четырехугольник можно вписать окружность

тогда и только тогда, когда

суммы длин противоположных сторон равны:

AD + BC = AB + CD.

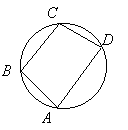7) около четырехугольника можно описать окружность

тогда и только тогда, когда

сумма противоположных углов равна 180⁰:

.

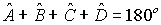• из всех параллелограммов только около прямоугольника

можно описать окружность;

- около трапеции можно описать окружность тогда и только тогда, когда она равнобокая;

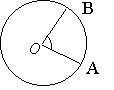8) центральный угол измеряется

градусной мерой дуги, на которую он опирается:

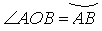
9) величина вписанного угла в два раза меньше

центрального угла, опирающегося на эту же дугу:

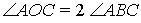
10) вписанные углы, опирающиеся на одну и ту же

дугу, имеют одинаковую величину: