Приведение произвольной системы сил к заданному центру

Приведем систему трех произвольно расположенных сил F ₁, F ₂ и F ₃, приложенных к твердому телу в точках А ₁, А ₂ и А ₃, к заданному центру О.

Получим три силы F ₁'', F ₂" и F ₃'', приложенные в центре О, и три присоединенные пары сил F ₁, F ₁', F _2, F ₂'и F ₃, F '₃ (рис.3.6). Складывая силы F ₁'', F ₂" и F ₃'' по правилу многоугольника, получим их равнодействующую R *, равную геометрической сумме заданных сил и приложенную в центре приведения О:

R ^* = F ₁''+ F ₂''+ F ₃'' = F ₁+ F ₂+ F ₃.

Геометрическая сумма всех сил системы называется главным вектором системы сил и в отличие от равнодействующей R обозначается R^*.

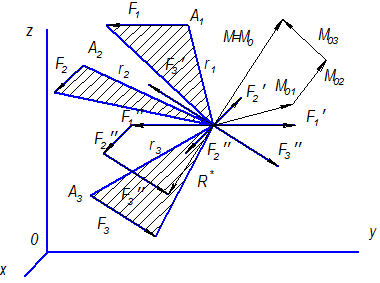
Рис. 3.6

Складывая пары F ₁ F ₁ ', F ₂, F '₂; F ₃, F '₃, получим эквивалентную им пару сил. Момент каждой присоединенной пары сил равен моменту соответствующей силы относительно центра приведения:

M ₁ = M ₁₀ = r ₁× F ₁; M ₂ = M ₂₀ = r ₂× F ₂; M ₃ = M ₃₀ = r ₃× F ₃.

Момент пары сил, эквивалентной трем присоединенным парам сил, равен геометрической сумме моментов этих пар.

Строя многоугольник моментов присоединенных пар, находим

M = M ₁+ M ₂+ M ₃ = M ₁₀+ M ₂₀+ M ₃₀ = M ₀ ,

т. е. момент пары сил, эквивалентной трем присоединенным парам, равен главному моменту этих трех сил относительно центра приведения.

Распространяя полученные результаты на любое число сил, произвольно расположенных в пространстве, имеем

R ^*= .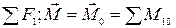

Этот результат можно сформулировать следующим образом: силы, произвольно расположенные в пространстве, можно привести к одной силе, равной их главному вектору и приложенной в центре приведения, и к паре сил с моментом, равным главному моменту всех сил относительно центра приведения.

Выбор центра приведения не отражается на модуле и направлении главного вектора R*, но влияет на модуль и направление главного момента М_о.

Пользуясь методом приведения произвольной системы сил к заданному центру, рассмотрим вопросы, связанные с системами сил, произвольно расположенных на плоскости.

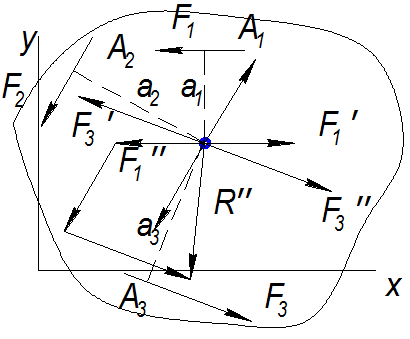
Рис. 3.7

Для вычисления главного вектора R* системы сил, произвольно расположенных на плоскости, воспользуемся методом проекций. На рис. 3.7 показано приведение к центру О трех сил F ₁ F ₂, F ₃. Известно, что

R ^*= F ₁+ F ₂+…+ F _n.

Обозначив R _x, R _y проекции главного вектора на оси координат, получим

R_x = F _{1 x} + F _{2 x} +…+ F_nx

R_y = F _{1 y} + F _{2 y} +…+ F_ny

где F _{1 x}, F _{2 x},..., F_nx; F _{1 y}, F _{2 y}, F _{n y} – проекции сил F ₁, F ₂, …, F _n соответственно на оси x и y.

Модуль и направление главного вектора R* определяются по формулам

.

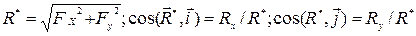Все присоединенные пары сил лежат в одной плоскости.

Момент эквивалентной им пары сил, равный главному моменту системы сил относительно центра приведения, определяется согласно как алгебраическая сумма моментов сил относительно этого центра.

М = М ₀= 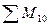.