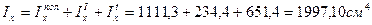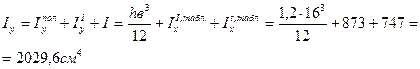Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
К задаче № 4.
|
|
Определить главные центральные моменты инерции сечения, составленного из прокатных профилей (рис. 14).
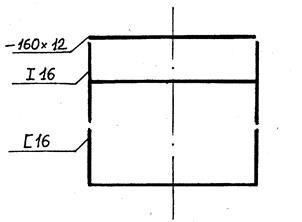
Рис. 14
Решение:
1. Вычертим сечение в масштабе, взяв необходимые размеры и характеристики в таблице сортамента (прил.1).
2. Покажем на схеме сечения центры тяжести составных частей (рис. 15).

Рис. 15
С1 – центр тяжести прямоугольной полосы;
С2 – центр тяжести двутавра;
С3 – центр тяжести швеллера.
Проводим центральные оси отдельных частей: х1, х2, х3, у1, у2, у3.
3. Определяем положение центра тяжести всего сечения в осях х0; у0 (ось х0 выбрана произвольно, у0 – совмещена с осью симметрии сечения).
Так как сечение симметрично относительно оси у0, то его центр тяжести расположен на этой оси.
Следовательно, координата хс центра тяжести составного сечения равна нулю, координату ус определим по формуле:

А1; А2; А3 – площади отдельных частей;
у1; у2; у3 – координаты центров тяжести отдельных частей.
А1=16х1, 2=19, 2 см2; А2=20, 2см2; А3=18, 1 см2
у1=6, 4+0, 6+8, 1=15, 1 см; у2=6, 4+4, 05=10, 45 см; у3=1, 8 см.
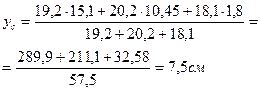
Показываем на чертеже центр тяжести сечения с (0; 7, 5) и проводим через него главные центральные оси х и у.
4. Вычислим расстояние между главной центральной осью всего сечения х и центральными осями отдельных частей х1; х2; х3 .
а1=15, 1-7, 5=7, 6 см
а2=10, 45-7, 5=2, 95 см а3=7, 5-1, 8=5, 7 см
5. На основании теоремы о зависимости моментов инерции относительно параллельных осей, одна из которых является центральной, вычисляем моменты инерции составных частей относительно оси х:

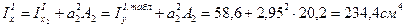
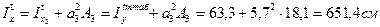
Таким образом, центральный осевой момент инерции сечения относительно оси х: