Исходные данные к задаче 4.

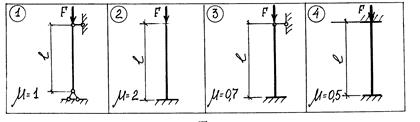Рис.4

Рис.5

Задача 5*. Для стального вала постоянного поперечного сечения с двумя зубчатыми колесами, передающего мощность Р КВт, при угловой скорости w, рад/с (числовые значения для своего варианта взять из таблицы 6). Определить диаметр вала, если 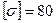Н/мм², а Frl=0, 4 х F1, Fr2=0, 4 х F2. Схемы для своего варианта – на рис.6.

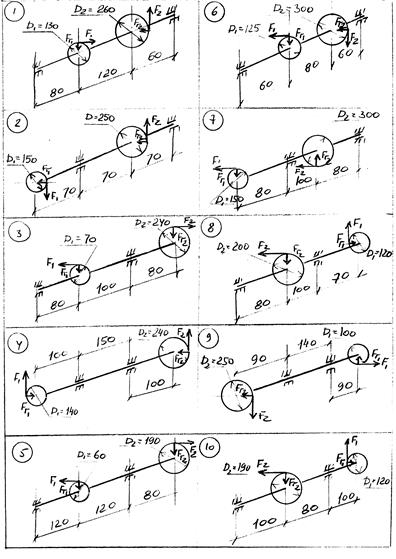
Таблица 5

Исходные данные к задаче 5.

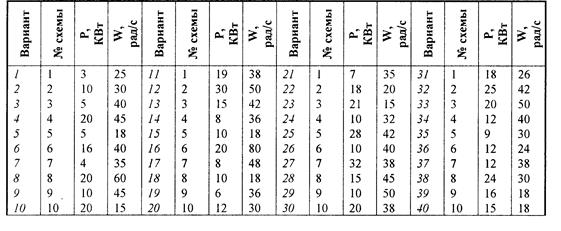РИС. 6

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ № 2.

К задаче 1. Двухступенчатый стальной брус нагружен силами F1, F2, F3 (рис. 7). Построить эпюры продольных сил N и нормальных напряжений d по длине бруса. Определить перемещение D 1 свободного края бруса (Е=2х10⁵ Н/мм²).

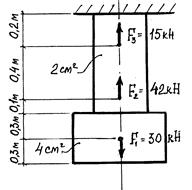Рис. 7

Решение: 1. Разбиваем брус на участки, начиная от свободного края. Границами участков будут сечения, в которых приложены силы (рис. 8).

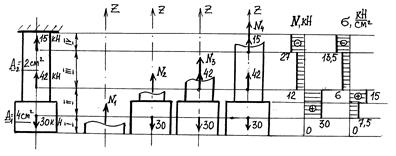Рис. 8

Данный брус имеет 4 участка. В пределах каждого участка воспользуемся методом сечений:

• Разбиваем брус на рассматриваемом участке сечением, перпендикулярным оси бруса;
• Мысленно отбрасываем любую часть бруса (лучше отбросить верхнюю часть с жесткой заделкой, чтобы не определять реакцию в защемлении);
• Заменяем влияние отброшенной части на оставленную внутренней силой Ni;
• Рассматриваем в равновесии оставленную (нижнюю) часть бруса под действием внешних сил и внутренней силы Ni;
• Составляем уравнение равновесия (уравнение статики Z: =0) и, решив его, определяем искомые внутренние силы.

Iуч.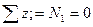

IIуч. 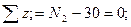N₂=30 кН

IIIуч. 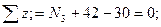N₃= - 12 кН

IVуч. 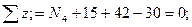N₄= -27 кН

По найденным значениям строим эпюру продольных сил.

2. Вычисляем ординаты эпюры нормальных напряжений

I уч.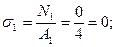

II уч.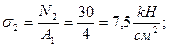

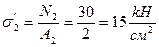
III уч.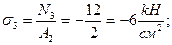

IV уч.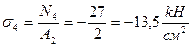

Строим эпюру нормальных напряжений.

3. Определяем перемещение свободного края как алгебраическую сумму абсолютных удлинений (укорочений) отдельных участков:

∆ l=∆ l₁+∆ l₂+∆ l^’₂+∆ l₃+∆ l₄= 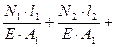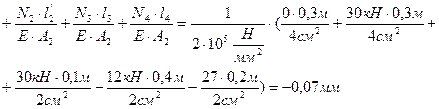(сжатие или укорочение).

К задаче 2. Для стальной балки, жестко защемленной с одного края, построить эпюры поперечных сил «Q» и изгибающих моментов «М» и подобрать из условия прочности необходимый размер двутавра, если 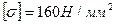(рис. 9).

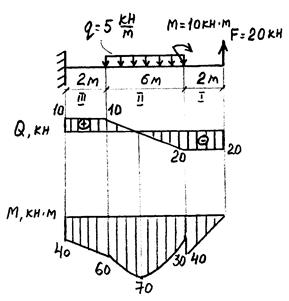
Рис. 9

Решение: 1. Делим балку на участки (3 участка: I, II, III). В пределах каждого участка воспользуемся методом сечений (см. задачу 1).

2. Запишем уравнения Q для каждого из трех участков, помня правило знаков:

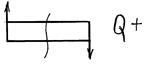Q1= -20

Q2= -20+5x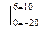

Q3= -20+5x6+10=10

Строим эпюру Q.

3. Запишем уравнения М для каждого из трех участков, помня правило знаков:

М1=20х

М2=20 (х+2)-10-5х²/2

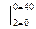
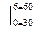
М3=20 (8+х)-10-5х6(3+х)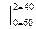

 

На участке с распределенной нагрузкой эпюра Q пересекает базу эпюры, следовательно, эпюру моментов, которая представляет собой параболу выпуклостью по стрелам нагрузки, следует строить, определив предварительно экстремальное значение момента. Для этого:

1. Приравняем к нулю уравнение Q на участке с распределенной нагрузкой: Q2= -20+5х=0; х=20/5; х=4;

2. Подставляем найденное значение х в уравнение М2. М2 экст. =20(4+2)-10-5х4²/2=70 КН х м.

3. Строим эпюру изгибающих моментов М.

4. Подбираем дутавр по таблице сортамента, определив требуемый момент сопротивления сечения.

 

W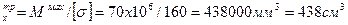

 

Принимаем I 30 W_х=472 см³ (прил. 1).

 

К задаче 3. Для заданной двухопорной балки построить эпюры поперечных сил и изгибающих моментов, подобрать круглое сечение (d-?) из условия прочности по нормальным напряжениям, если 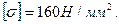Проверить жесткость подобранного сечения (по таблицам), если модуль упругости Е=2х10⁵ Н/мм², а допустимый прогиб .

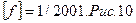Решение: 1. Перед тем, как строить эпюры, определим реакции в опорах, составив уравнение статики:

 

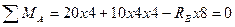
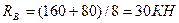
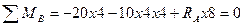
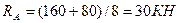
Проверка: 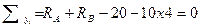; 30+30-60=0

Следовательно, реакции в опорах определены верно. Строим эпюру «Q» (поперечных сил), помня правило знаков:

 

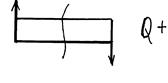QI= -30

QII= -30+10x

QIV=30

QIII=30-10x

Строим эпюру «М» (изгибающих моментов):

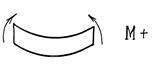МI = 30х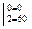

МII = 30(2+х)-10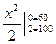

МIV = 30х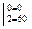

МIII = 30(2+х)-10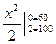

 

 

Эпюра «М» строится на растянутых волокнах.

 

Рис. 10

3. Из условия прочности по допускаемым нормальным напряжениям подбираем сечение.

 

 

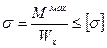
Требуемый момент сопротивления сечения: W_х= 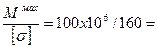625000 мм³

 

Для круглого сечения W_x=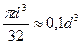

 

Следовательно, d= 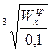= =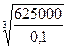184 мм 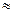19 см;

 

 

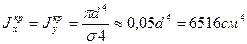
4. Для проверки жесткости подобранного сечения необходимо определить максимальный прогиб балки и сравнить его с допустимым прогибом. (f)=1/2001=800/200=4 см=40 мм.

 

По таблице 3 приложения определим сначала максимальный прогиб балки от силы F=20КН:

 

 

 

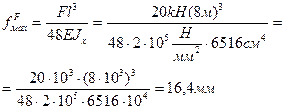
Максимальный прогиб балки от распределенной нагрузки q (прил. 3):

 

 

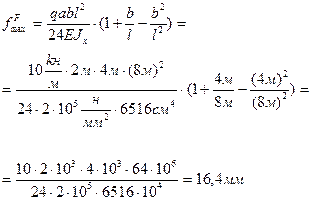
Полный максимальный прогиб балки круглого сечения диаметром 19 см:

 

 

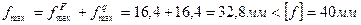
Следовательно, жесткость обеспечена.

 

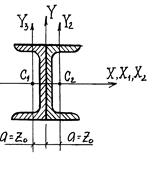
К задаче 4. Подобрать сечение центрально-сжатой колонны сплошного сечения, составленного из швеллеров, соединенных в сплошное сечение при помощи сварки.

Принять 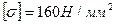(рис. 11).

 

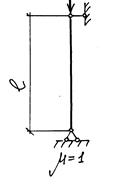Рис. 11

Решение: условие устойчивости стойки имеет вид: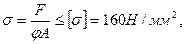

где F – продольная сила, А – площадь поперечного сечения колонны, φ – коэффициент продольного изгиба, зависящий от материала стержня и его гибкости.

 

Подбор сечения производим методом приближений.

Для первого приближения примем φ =0, 7. Тогда требуемая площадь сечения: А_тр=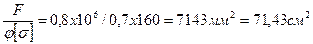

 

Требуемая площадь сечения одного швеллера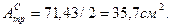

По таблице сортамента (прил. 1) принимаем [ 30 для которого А = 40, 5 см²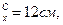, i i 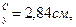Z₀=2, 52 см.

Радиусы инерции составного сечения: i_х= 12 см, = i

i_у=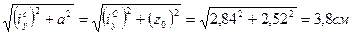

вычисляем гибкость стойки: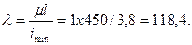

 

По таблице зависимости φ от λ (приложение 2) определяем значение коэффициента продольного изгиба методом интерполяции φ =0, 52-(0, 52-0, 45)/10х8, 4=0, 46.

 

Проверяем условие устойчивости: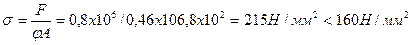

Получено перенапряжение.

 

Во втором приближении:

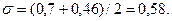
Требуемая площадь сечения: А_тр=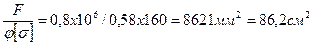

Требуемая площадь сечения одного швеллера А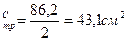

По таблице сортамента (приложение 1) принимаем [33, для которого А=46, 5 см²,

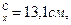i i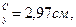

 

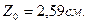
Радиусы инерции составного сечения: i_х=i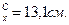

 

 

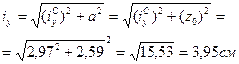
Вычисляем гибкость стойки: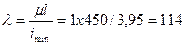

По таблице (приложение 2) определяем коэффициент продольного изгиба: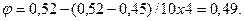

 

Проверяем условие устойчивости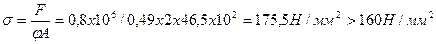

В третьем приближении 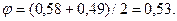Требуемая площадь сечения А_тр=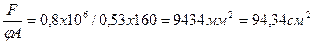

 

Требуемая площадь одного швеллера: А

 

По таблице сортамента (приложение 1) принимаем

[36 А^[ =53, 4 см².

i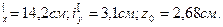

Радиусы инерции составного сечения: i_х=i ;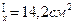

 

i_у=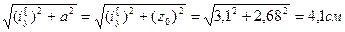

 

вычисляем гибкость стойки: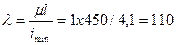

По таблице (приложение 2) определяем коэффициент продольного изгиба: .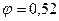

Проверяем условие устойчивости: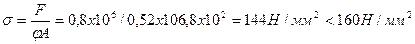

Окончательно принимаем сечение стойки из двух швеллеров 36.

⇐ Предыдущая14151617181920212223Следующая ⇒

Поделиться с друзьями: