Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
К задаче 3.
|
|
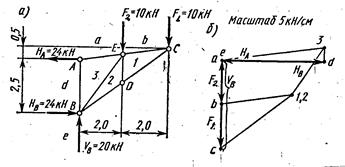
Условие задачи. Определить силы в стержнях статически определимой фермы (рис. 1, а) путем построения диаграммы Максвелла-Кремоны.
Решение. Чертеж фермы необходимо выполнить, четко соблюдая заданные размеры в принятом масштабе. Приложим заданные внешние силы 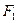 и
и 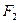 и опорные реакции
и опорные реакции 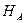 и
и 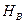 . Плоскость чертежа между внешними приложенными силами – внешние поля, обозначим a, b, c, e, d, обходя ферму по часовой стрелке. Плоскость чертежа, ограниченную стержнями, - внутренние поля обозначим цифрами 1, 2, 3. В дальнейшем каждую внешнюю и внутреннюю силу будем обозначать двумя значками, соответствующими наименованию тех смежных полей, границами которых они являются, называя эти буквы в порядке обхода фермы по часовой стрелке. Так сила
. Плоскость чертежа между внешними приложенными силами – внешние поля, обозначим a, b, c, e, d, обходя ферму по часовой стрелке. Плоскость чертежа, ограниченную стержнями, - внутренние поля обозначим цифрами 1, 2, 3. В дальнейшем каждую внешнюю и внутреннюю силу будем обозначать двумя значками, соответствующими наименованию тех смежных полей, границами которых они являются, называя эти буквы в порядке обхода фермы по часовой стрелке. Так сила 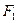 будет обозначаться a – b. Сила в стержнях фермы – либо двумя цифрами, либо буквой и цифрой по наименованию смежных полей, соблюдая при этом правило обхода узла по часовой стрелке. Так, сила стержня ЕС будет обозначаться b – 1 или (1 - b), смотря по тому, какой узел мысленно вырезаем–узел Е или узел С. Первая буква или цифра в обозначении силы в стержне та, которая встречается первой при обходе узла по часовой стрелке. Выбираем масштаб сил. Например, 5 кН/см (5 кН в одном см). От произвольной точки а в принятом масштабе откладываем внешнюю силу a – b (рис. 1, б), затем b – c; от точки с вертикально вверх откладываем реакцию с – е. Так как сумма значений сил
будет обозначаться a – b. Сила в стержнях фермы – либо двумя цифрами, либо буквой и цифрой по наименованию смежных полей, соблюдая при этом правило обхода узла по часовой стрелке. Так, сила стержня ЕС будет обозначаться b – 1 или (1 - b), смотря по тому, какой узел мысленно вырезаем–узел Е или узел С. Первая буква или цифра в обозначении силы в стержне та, которая встречается первой при обходе узла по часовой стрелке. Выбираем масштаб сил. Например, 5 кН/см (5 кН в одном см). От произвольной точки а в принятом масштабе откладываем внешнюю силу a – b (рис. 1, б), затем b – c; от точки с вертикально вверх откладываем реакцию с – е. Так как сумма значений сил 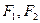 равна значению силы
равна значению силы 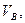 точка е совпадает с точкой а. Затем из точки е проводим прямую, параллельную
точка е совпадает с точкой а. Затем из точки е проводим прямую, параллельную 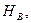 и откладываем от нее реакцию e – d и, наконец, из точки d в обратном направлении откладываем реакцию d – a. В результате получаем замкнутый силовой многоугольник abceda. Далее, последовательно рассматривая узлы, строим диаграмму сил, возникающих в стержнях.
и откладываем от нее реакцию e – d и, наконец, из точки d в обратном направлении откладываем реакцию d – a. В результате получаем замкнутый силовой многоугольник abceda. Далее, последовательно рассматривая узлы, строим диаграмму сил, возникающих в стержнях.
Построение диаграммы начинаем с узла С, где сходятся лишь два стержня. Стержни этого узла расположены между тремя полями: двумя буквенными и одним цифровым. На силовой линии есть уже точки, соответствующие буквенным полям. Проводим через точку с прямую, параллельную стержню с – 1, а через точку b – прямую, параллельную стержню 1 – b. Пересечение этих линий дает точку 1, соответствующую внутреннему полю между рассматриваемыми стержнями и примыкающему к рассматриваемому узлу. Строим точку 2. Цифра 2 входит в название стержней с – 2 и 2 – 1, принадлежащих узлу D. Узел D можно вырезать, так как силы в двух стержнях неизвестны, а в третьем – найдены при рассмотрении первого узла. Из точки 1 диаграммы проводим линию, параллельную стержню 2 – 1, а из точки С – линию, параллельную с – 2. Точка 2 совпадет с точкой 1. Это означает, что сила в стержне 2 – 1 равна нулю. Вырезаем узел Е, где сходятся четыре стержня, в двух из них силы можно определить по диаграмме, а в двух (2 – 3 и 3 - а) неизвестны. Строим точку 3. Для этого из точки 2 проводим прямую, параллельную стержню 2 –3, а из точки а – параллельную 3 – а. На их пересечении получаем точку 3.
Значения сил в стержнях определяем, измеряя длины линии на диаграмме с учетом принятого масштаба сил. Знак силы определяется следующим образом: Начинаем с узла С, обходя его по часовой стрелке. Прочитывая на диаграмме обозначение стержня 1 – b делаем движение по линии, обозначающей силу в стержне от одной точки к другой в соответствии с названием. Это движение переносим на стержень фермы, совмещая начало движения с рассматриваемым узлом. Если движение при этом направлено по стержню от узла, стержень считается растянутым, а если к узлу– то сжатым. Итак, 1– b – от узла, стержень растянут, N=16 кН; с – 1 – к узлу, стержень сжат, N=20 кН; 1 – 2 – стержень не работает, N=0; с – 2 – к узлу, стержень сжат, N=20 кН; 2 – 3 – к узлу, стержень сжат N=13 кН; 3 – а – от узла, стержень растянут N=24 кН и т.д.
|
РИС.9
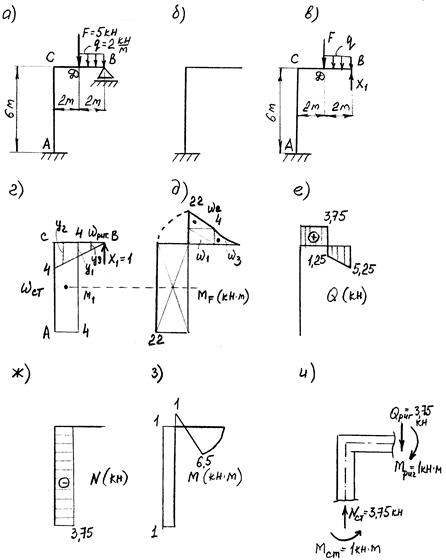
К задаче 4.
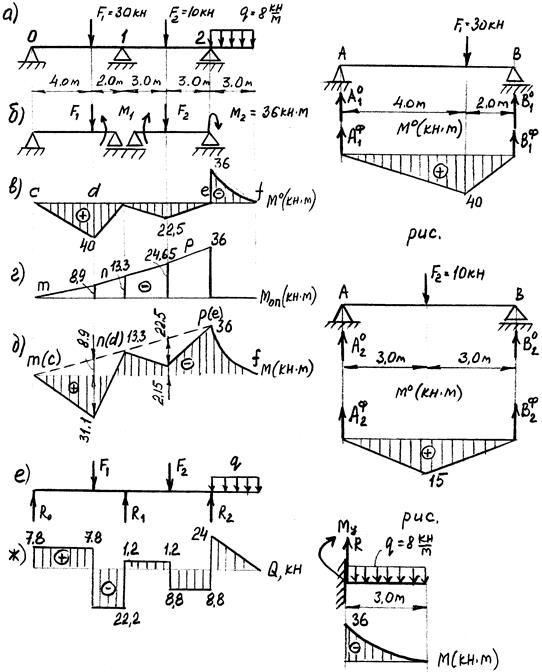
Условие задачи. Для балки (рис.11а) построить эпюры М и Q с использованием уравнения трех моментов.
Решение.
1. Прономеруем опоры 0, 1, 2 и пролеты l1, l2 (номер пролета ставится на опоре справа).
2. Определим степень статической неопределимости по формуле: Л=Сon-3=4-3=1 – балка один раз статически трех моментов.
3. Изобразим основную систему: для этого введем шарнир в промежуточное опорное сечение (опора 1) и нагрузим ее заданной нагрузкой и неизвестным опорным моментом М1 (рис.11б). Консоль отбросим, заменив ее действие на оставшуюся часть моментом М2=q× 3× 1, 5=8× 3× 1, 5=36 кН.
4. Рассмотрим пролеты неразрезной балки, как простые балки на двух шарнирных опорах и вычислим для каждого пролета действительные опорные реакции (А° и В°), фиктивные опорные реакции (Аф и Вф) с помощью форму приложения и построим эпюры изгибающих моментов от заданной нагрузки М°:
а) пролет 1 (рис.12) 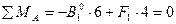

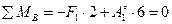
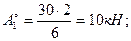

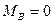
 сечF1=
сечF1= 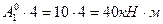

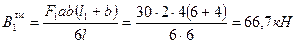
б) пролет 2 (рис.13) 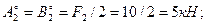
МсечF2= 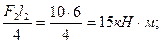
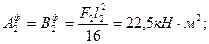
в) консоль рассматриваем как балку, заделанную левую концом (рис.14). Момент заделке
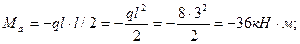

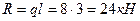
5. Изобразим эпюру моментов М° (см.рис.11, в) от пролетной нагрузки исходя из рассмотренных разрезных балок.
6. Составим управление трех моментов для опоры l.
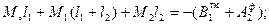
М0 = 0; М2 = -36кН·м – момент, заменяющий действие отброшенной консоли. После подстановки значений получим
2М1(6 + 6) – 36 · 6 = -6(66, 7 + 22, 5);
24М1 = -319, 2; М1 = -13, 3кН·м
Строим эпюру опорных элементов Моп (рис.11г) от нагружения разрезных балок только опорными моментами. Отрицательные ординаты откладываем вверх, а положительные – вниз.
7. Строим суммарную эпюру изгибающих моментов. Ординаты суммарной эпюры вычисляем алгебраическим сложением ординат эпюр М° и Моп. Можно воспользоваться графическим приемом, который называют способом «подвешивания» эпюр (рис.11д). Для этого совмещаем точки с, d, e эпюры М° соответственно с точками m, п, р – вершинами линии опорных моментов, т.е. как бы подвешивает эти эпюра нулевыми точками к вершинам линии опорных моментов снизу. Эпюру моментов консольной части даем отдельно. Окончательные ординаты суммарной эпюры вычисляют также алгебраическим сложением ординат эпюр М ° и Моп (см.рис.11, д).
8. Определяем опорные реакции неразрезной балки по формуле:
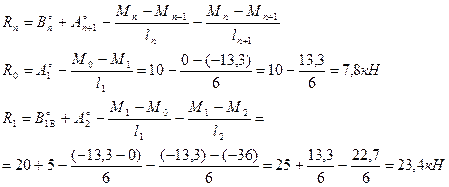
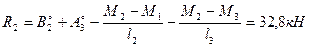
9. С учетом полученных значений оперных реакций определяем поперечные силы в характерных сечениях рассматриваемой балки:
Ход слева:
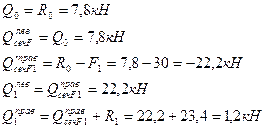

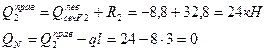
По найденным значениям поперечных сил строим эпюру «Q» рис.11, ж.
|
|
|
|
ПРИЛОЖЕНИЕ 5
Значение коэффициентов продольного изгиба
| Гиб-кость | Ст3, Ст4 | Ст5 | Чугун | Дерево (сосна, ель) | Гиб-кость | Ст3, Ст4 | Ст5 | Чугун | Дерево (сосна, ель) |
| 0.45 | |||||||||
| 0, 99 | 0, 98 | 0, 97 | 0, 99 | 0, 40 | |||||
| 0, 97 | 0, 96 | 0, 91 | 0, 97 | 0, 36 | |||||
| 0, 95 | 0, 93 | 0, 81 | 0, 93 | 0, 32 | |||||
| 0, 92 | 0, 90 | 0, 69 | 0, 78 | 0, 29 | |||||
| 0, 89 | 0, 85 | 0, 57 | 0, 80 | 0, 26 | |||||
| 0, 86 | 0, 80 | 0, 44 | 0, 71 | 0, 23 | |||||
| 0, 81 | 0, 74 | 0, 34 | 0, 61 | 0, 21 | |||||
| 0, 75 | 0, 67 | 0, 26 | 0, 49 | 0, 19 | |||||
| 0, 69 | 0, 59 | 0, 20 | 0, 38 | 0, 17 | |||||
| 0, 60 | 0, 50 | 0, 16 | 0, 31 | 0, 16 | |||||
| 0, 52 | 0, 43 | - | 0, 25 |
ПРИЛОЖЕНИЕ 6