К задаче 2.

Условие задачи. Построить эпюры M_x, Q, N методом сил для статически неопределимой рамы. (рис.9а)

Известно, что при определении степени статической неопределимости рам удобно пользоваться формулой Л = С_оп -3, где Л - степень статической неопределимости системы, равная числу лишних связей; С_оп - число опорных стержней; 3- число уравнений статики. Поскольку жесткое защемление эквивалентно трем опорным стержням плюс один стержень (подвижная опора), получаем С_оп =4. Подставим значения, получим Л =4-3=1.

Имеем одну лишнюю неизвестную или рама один раз статически неопределима.

Дальнейший расчет ведем методом сил, для чего прежде всего необходимо выбрать основную систему. Для этого надо отбросить лишнюю связь и действующую нагрузку. Удачный выбор основной системы упрощает расчет. Для данной задачи наиболее выгодно устранить шарнирно-подвижную опору, получив таким образом геометрически неизменяемую статически определимую консольную раму - основную систему (рис.9 б).

Для получения нагруженной системы приложим к основной внешнюю заданную нагрузку и лишнюю пока неизвестную реакцию Х₁, приложенную по направлению отброшенной связи (рис.9в) и заменяющую действие на раму этой связи. Далее составляем каноническое уравнение для определения Х₁

diiXi+Dip= 0,

которое выражает условие равенства нулю вертикального перемещения точки В от совместного действия неизвестной Хi и заданной нагрузки. Перемещения, входящие в канонические уравнения в качестве коэффициентов при неизвестных и свободных членах вычисляют, используя правило Верещагина, учитывая, что эпюры, подлежащие перемножению, соответствуют индексам при d и D. Вычисляем перемещения dii и Dip, для чего строим эпюры M_i и M_F.

а) Эпюра M_i (рис.9 г). Нагрузим основную только силой X_i1. Поскольку рама с консолью, то, не определяя опорных реакций в заделке, можно построить эпюру М ходом со свободного конца по характерным точкам. M_B =0; M_C=X_il = 1х4=4 кНхм; M_A=X_il=4 кНхм.

б) Эпюра М_F(рис.9 д). Нагрузим основную систему только заданной нагрузкой. Эпюра моментов уже построена. Перенесем ее из предыдущей задачи.

По данным построения эпюр M_i и M_F находим dii и Dip.

в) dii - перемещение точки В от единичной нагрузки Xi =1 по направлению действия силы Xi определяется по формуле dii =( 1/ EIx)wy умножением эпюры Mi самой на себя; по этой причине dii всегда положительно; w - площадь эпюры моментов от единичной нагрузки Xi =1; y - ордината той же эпюры Mi, лежащая под центром тяжести площади эпюры. Произведение EIx жесткость сечения элементов рамы. Считаем ее постоянной для всей рамы.

dii = 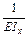(w_ригy_риг+w_СТy_СТ)= 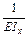( х4х4х2, 67+4х6х4)=117, 4 ,

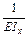имея в виду, что w_риг - площадь треугольной эпюры M_1риг; w_риг =1/2 bh = 1/2х4х4; w_CT = bh =4õ 6; y_риг =2, 67 - ордината эпюры М₁,

соответствующая положению центра тяжести треугольника; y_СТ =4 - соответствующая ордината прямоугольной эпюры М₁ стойки.

г) Dip -перемещение точки В по направлению действия Xi от заданной нагрузки определяется по той же формуле, что и dii, но перемножением эпюр M_F и M₁. Перемножая эпюры M_F и M₁, площади w возьмем из эпюры M_F, причем, если эпюра имеет сложное очертание, ее необходимо расчленить на простые фигуры, для которых известны формулы площадей и координаты их центров тяжести. Эпюру M_Fриг разбиваем на прямоугольник - площадь 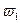, треугольник - 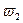и площадь, параболической кривой - 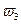плюс прямоугольная эпюра на стойке - 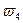. Ординаты 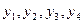возьмем на эпюре моментов от единичной нагрузки, расположенными под соответствующим центрами тяжести площадей грузовой опоры эпюры моментов M_F (рис.9 г, д).

Dip = 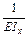(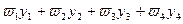)=- 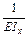(4х2х3+ 18х2х3.33+

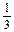+ х4х2х 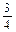х2+22х6х4)=-(1/EIx)616.

Поскольку эпюры M_F и M₁ расположены по разные стороны от оси стержня, их произведение берется со знаком минус.

д) Находим Х₁, подставляя полученные dii и Dip в каноническое уравнение:

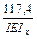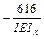Х₁+()=0.

Отсюда Х₁, =616/117, 4=5, 25 кН. Положительный результат означает, что направление реакции Х₁ правильно.

е) Строим окончательные эпюры Q, M, и N обычным путем, нагрузив основную систему кроме заданной нагрузки уже известной силой Х₁ =5, 25 кН.

Эпюра N: (рис.9ж)

N^I = N^II = 0; N^III = - F – q · 2 + x₁ = -5 – 2 · 2 + 5, 25 = - 3, 75 кН

Эпюра Q: (рис.9е)

Q^I = - x₁ + q·x = -5, 25 + 2x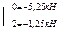

Q^II = -x₁ + q·2 + F = -5, 25 + 2·2 + 5 = 3, 75 кН

Q^III = 0.

Эпюра М: (рис.9з)

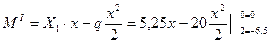
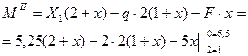
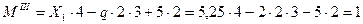
Строим эпюру М_х (рис.1, к). Чтобы убедиться правильности построения эпюры М, нужно вычислить перемещение точки В по направлению отброшенной связи. Для этого необходимо перемножить окончательную эпюру М_х и М₁. Если найденное перемещение равно нулю, то эпюра М_х построена правильно. Жесткость узла С проверяется как в статически определимой раме. Достаточно взглянуть на чертеж узла С с приложенными к нему силовыми факторами (рис.9и), чтобы убедиться в равновесии узла, не составляя уравнений равновесия. При сравнении эпюр статически определимой рамы с окончательными эпюрами статически неопределимой видно, что у последней внутренние силовые факторы M, Q, N получились меньшими.