Работа четырехполюсника на нагрузку

Из основных уравнений четырехполюсника (1.123), видно что ток и напряжение на первичных зажимах состоят из двух слагающих, а именно:

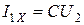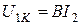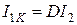; при ;

; при 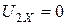. (1.153)

Если подставить (1.153) в (1.123), получим:

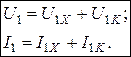(1.154)

Уравнение (1.154) выражают основной принцип наложения в электрической цепи.

Рассмотрим теперь передачу энергии через пассивный четырехполюсник.

Определим соотношение между сопротивлением нагрузки 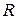и коэффициентами 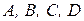четырехполюсника, при которых величина КПД будет максимальной, см. рисунок 1.66.

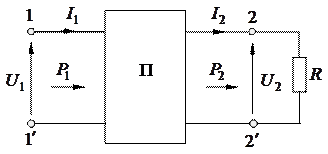Рисунок 1.66 - Передача энергии через пассивный четырехполюсник

Из рисунка 1.66 видно, что:

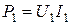- входная мощность на первичных зажимах;

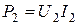- выходная мощность на вторичных зажимах.

Коэффициент полезного действия определится так

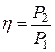. (1.155)

Под КПД пассивного четырехполюсника 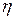понимается отношение мощности на входе к мощности на его выходе.

Запишем 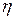в функции от коэффициентов, имеем:

;

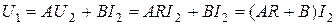. (1.156)

Мощность на выходных зажимах будет

. (1.157)

Мощность на входных зажимах найдется

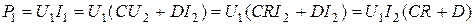. (1.158)

Подставим в (1.158) выражение (1.156), получим, мощность на входе цепи

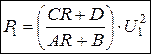. (1.159)

Тогда КПД определится так:

;

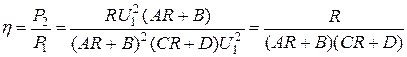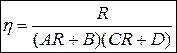. (1.160)

Величину сопротивления 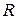, при котором КПД имеет максимум определяется обычным образом. Из математики известно, что

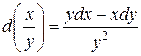, поэтому,

.

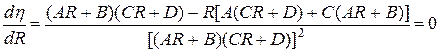Знаменатель величина больше нуля, поэтому приравнивая числитель полученного выражения к нулю, имеем

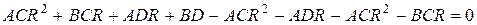, приводя подобные члены получаем

.

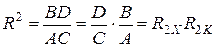Окончательно можем записать

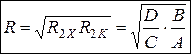. (1.161)