
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Примеры решения задач. Задача 1. Три одинаковых положительных заряда q1= q2=q3=1нКл расположены по вершинам равностороннего треугольника
|
|
Задача 1. Три одинаковых положительных заряда q1= q2=q3=1нКл расположены по вершинам равностороннего треугольника. Какой отрицательный заряд q4 нужно поместить в центре треугольника, чтобы сила притяжения с его стороны уравновесила силы взаимного отталкивания зарядов, находящихся в вершинах?
| Дано: q1=q2=q3=1нКл | 1· 10-9 Кл | Решение. Физическую систему составляют четыре заряда, расположенные так, как показано на рис. |
| q4-? |
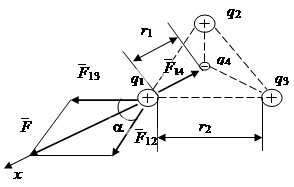
Рис.1.1
Так как три заряда, расположенные в вершинах, находятся в одинаковых условиях, достаточно рассмотреть равновесие одного из них, например q1. На рис. показаны силы, действующие на заряд q1. Со стороны зарядов q2, q3, q4 – соответственно `F12, `F13, `F14.
Запишем условия равновесия:
`F12+`F13+`F14=`F+`F14=0, (1.10)
где `F – равнодействующая сил `F12 и `F13.
Уравнение (1) запишем в проекциях на ось 0Х:
F-F14=0 или F=F14. (1.11)
Найдём F по теореме косинусов (см. рис.1.1) с учётом, что из (1.1) 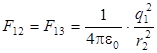 ,
,
 . (1.12)
. (1.12)
F4 – можно определить по закону Кулона (1.1):
 . (1.13)
. (1.13)
Из геометрических соображений
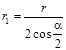 (1.14)
(1.14)
Приравняем (1.12) и (1.14) с учётом того, что в равностороннем треугольнике a = 60° и принимая во внимание (1.14):
 (1.15)
(1.15)
Отсюда получим 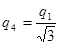 .
.
Подставим численное значение:
q4 = 0, 58 нКл.
Ответ: q4 = 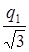 = 0, 58 нК.
= 0, 58 нК.
Задача 2. Два заряда 9q и –q закреплены на расстоянии 1м друг от друга. Третий заряд q1 может перемещаться только вдоль прямой, проходящей через заряды. Определить положение заряда q1, при котором он будет находиться в равновесии. При каком знаке заряда равновесие будет устойчивым?
| Дано: 9q q1 -q l =1м | Решение. Физическая система состоит из трёх зарядов. Рассмотрим равновесие заряда q1. Векторная сумма сил, действующих на него, будет равна нулю. Покажем на рис. три возможных случая расположения заряда q1 по отношению к 9q и –q, а также силы, действующие на него в каждом из этих трёх случаев. |
| х -? |
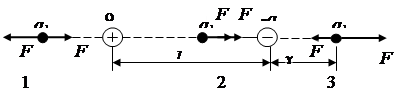
Рис.
Из рис. видно, что в случае 2 векторная сумма сил отличная от нуля, т.к. силы действующие со стороны заряда 9q и –q, соответственно`F+ и `F- направлены одинаково. Силы взаимодействия двух точечных зарядов пропорциональны величинам зарядов и обратно пропорциональны расстоянию между ними. Следовательно, в случае 2 |F+| > ê F-ê, т.к. положительный заряд 9q больше отрицательного по модулю и расположен к q1 ближе, чем заряд -q. Остаётся записать условия равновесия для случая 3:
 или |F+ | = |F- |
или |F+ | = |F- |
Используем закон Кулона (1.1):
 .
.
Отсюда, после сокращений и извлечения квадратного корня получим:
l + x= ± 3x или x1= l /2, x2= - l /4
Корень x2 не удовлетворяет физическому условию задачи (см. рис. случай 2). Подставим числовое значение: х = 0, 5м. Определим знак заряда, при котором равновесие будет устойчивым. Равновесие называется устойчивым, если при смещении заряда от положения равновесия возникают силы, возвращающие его в положение равновесия. Рассмотрим смещение заряда q1 в двух случаях: 1) заряд положителен и 2) заряд отрицателен. Если заряд q1 положителен, то при смещении его влево обе силы `F+ и `F- возрастают. Но, `F+ возрастает медленнее (заряд 9q всегда находится дальше, чем -q), следовательно, `F- по модулю больше чем F+, и на заряд q1 будет действовать результирующая сила, направленная от положения равновесия. То же происходит и при смещении заряда вправо.
Таким образом, в случае положительного заряда равновесие является не устойчивым.
1) если заряд q1 отрицателен, то его смещение влево вызовет увеличение сил F+ u F-, но сила F+ возрастает медленнее, чем F-, т.е. | F+| < |F-|. Следовательно, результирующая сила направлена к положению равновесия. При смещении вправо результат будет таким же. При отрицательном заряде равновесие будет устойчивым, величина заряда q1 несущественна.
Примечание. В электростатике устойчивое равновесие возможно только при определённых ограничениях. В рассматриваемом примере заряд q1 может перемещаться только вдоль прямой, проходящей через заряды q u –9q. При снятии этого ограничения устойчивое равновесие не возможно.
Ответ: х= l / 2=0, 5м. Равновесие будет устойчивым, если q1 - отрицателен.
Задача 3. Тонкий стержень длиной 30см несёт равномерно распределённый по длине заряд с линейной плотностью 1мкКл/м. На расстоянии 20см от стержня находится заряд 10мкКл равноудалённый от концов стержня. Определить силу взаимодействия точечного заряда с заряженным стержнем.
| Дано: l= 30cм r0=20см t=1мкКл/м q=10мкКл | 0, 3м 0, 2м 10-6Кл/м 10-8Кл |
Решение.
Физическая система, которую мы будем рассматривать, состоит из стержня и точечного заряда, находящегося в поле стержня. Найдем силу, действующую на точечный заряд. Эту силу можно выразить через напряжённость  поля поля
|
| F -? |
заряженного стержня в точке 0, где находится точечный заряд (см. рис.1.3):
 (1.19)
(1.19)
Будем рассматривать стержень как совокупность точечных зарядов. Для этого разобьём его на дифференциально малые участки dl с зарядом dq=tdl. Сначала найдём напряжённость 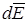 такого точечного заряда, а затем используя принцип суперпозиции (1.6) напряженность поля всего стержня. Покажем на рис.1.3 выделенный элемент и напряженность
такого точечного заряда, а затем используя принцип суперпозиции (1.6) напряженность поля всего стержня. Покажем на рис.1.3 выделенный элемент и напряженность 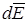 создаваемого им поля, и разложим
создаваемого им поля, и разложим 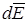 на два перпендикулярных вектора
на два перпендикулярных вектора 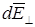 (перпендикулярный стержню) и
(перпендикулярный стержню) и  (параллельный стержню).
(параллельный стержню).
Тогда в соответствии с (1.6):

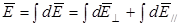
Для участков dl, расположенных на стержне симметрично относительно ОА, вектор  будет иметь направление, противоположное указанному на рисунке. Следовательно, эти векторы в сумме дадут ноль, и ò
будет иметь направление, противоположное указанному на рисунке. Следовательно, эти векторы в сумме дадут ноль, и ò 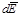 // = 0.
// = 0.
Тогда 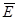 =ò
=ò 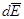 ^ и, следовательно, результирующий вектор будет направлен перпендикулярно стержню, а модуль его
^ и, следовательно, результирующий вектор будет направлен перпендикулярно стержню, а модуль его
 . (1.21)
. (1.21)
Из рис.1.3 видно: 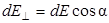 . Напряженность точечного заряда dq (1.4):
. Напряженность точечного заряда dq (1.4):

Из геометрических построений (рис.1.3): 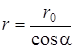 ,
, 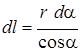 ,
, 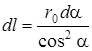 .
. 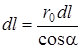 (1.23)
(1.23)
Подставим: 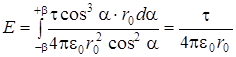 ·
·  . (1.24)
. (1.24)
Из геометрических соображений:
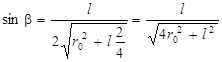 (1.25)
(1.25)
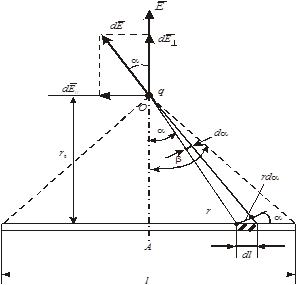
Рис.
Подставим (1.25) в (1.24) и получим напряженность поля в точке, где находится заряд q:
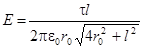 . (1.26)
. (1.26)
Тогда сила, действующая на заряд (1.19):
F=  . (1.27)
. (1.27)
После подстановки числовых значений: F= 0, 54 мН.
Ответ: F= 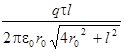 = 0, 54 мН и направлена перпендикулярно стержню, от него.
= 0, 54 мН и направлена перпендикулярно стержню, от него.
Задача 4. Электрическое поле создано бесконечной плоскостью, заряженной с поверхностной плотностью 400нКл/м2 и бесконечной прямой нитью, заряженной с линейной плотностью 100нКл/м. На расстоянии 10см от нити находится точечный заряд 10нКл. Определить силу действующую на заряд, её направление, если заряд и нить лежат в одной плоскости, параллельной заряженной плоскости.
| Дано: s =400нКл/ м2 t =100нКл/м q =10нКл r = 10см | 4× -10-7 л/м2 10-7 Кл/ м 10-8 Кл 0, 1м |
Решение.
Рассмотрим физическую систему, состоящую из заряженных плоскости, нити и точечного заряда q, помещенного в их поле. На заряд, помещенный в электрическое поле с напряженностью 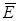 , действует сила `F (1.3): , действует сила `F (1.3):
|
| F -? |


 `
` 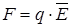 (1.28)
(1.28)
Найдем напряженность поля, создаваемого плоскостью и нитью. Согласно принципу суперпозиции (1.6):
 (1.29)
(1.29)
где  - напряженность поля плоскости,
- напряженность поля плоскости,  - напряженность поля нити;
- напряженность поля нити;

 (1.30)
(1.30)

 Направление векторов покажем на рис.1.4. Так как векторы
Направление векторов покажем на рис.1.4. Так как векторы 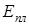 и
и  перпендикулярны, то Е=
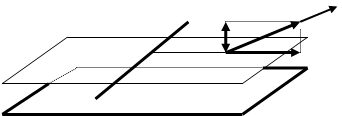
перпендикулярны, то Е= 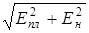 или с учетом (1.30)
или с учетом (1.30)
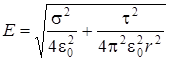 .
.
 |
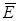 пл
пл 
τ 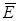
r

Рис.1.4
Тогда сила, действующая на заряд, согласно (1.28):

После подстановки числовых значений получим: F =289 мкН.
Направление силы задаётся углом a к заряженной плоскости (см. рис.1.4.):

откуда  51º 34'.
51º 34'.
Ответ:  =289 мкН, направлена под углом
=289 мкН, направлена под углом 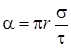 =51º 34' к заряженной плоскости.
=51º 34' к заряженной плоскости.
Задача 5. Найти напряженность электрического поля в центре полукольца радиусом R=5см, по которому равномерно распределен заряд q=3× 10-9Кл.
| Дано: R=5см q=3× 10-9Кл | 0, 05м | Решение. Физическую систему составляют: заряженное полукольцо и электрическое поле заряда q этого заряда. Для определения напряженности воспользуемся принципом суперпозиции. Разделим полукольцо на малые элементы ду- |

|
ги dl так, чтобы заряд dq = tdl / (π R) каждой такой дуги можно было считать точечным. Для равномерного распределения заряда t - линейная плотность заряда полукольца:
 (1.31)
(1.31)
Выберем два произвольных симметрично расположенных относительно 00' элемента дуги (рис. 1.5). Напряженности электрического поля в точке 0, создаваемые выбранными элементами d  и d
и d 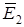 согласно принципу суперпозиции
согласно принципу суперпозиции
d 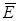 = d
= d  + d
+ d 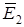 .
.

Рис.1.5
Из соображений симметрии следует, что алгебраическая сумма проекций напряженности поля выбранных элементов на ось Оy равна нулю. Результирующее поле направлено вдоль оси Ох:

Так как 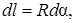 то
то 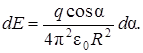 Положение точечного заряда
Положение точечного заряда 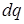 на полукольце определяется углом α. Поэтому угол α и выберем в качестве переменной интегрирования:
на полукольце определяется углом α. Поэтому угол α и выберем в качестве переменной интегрирования:
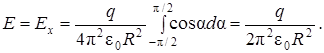
Подставив численные значения величин, получим Е = 6, 88· 103 В/м.
Ответ: 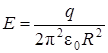 = 6, 88· 103 В/м.
= 6, 88· 103 В/м.
Задача 6. Покажите и рассчитайте поле равномерно заряженной бесконечной плоскости.
Поле равномерно заряженной бесконечной плоскости. Бесконечная плоскость (рис. 1.17) заряжена с постоянной поверхностной плотностью + 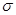 (
( - заряд, приходящийся на единицу поверхности).
- заряд, приходящийся на единицу поверхности).

Рис. 1.17
Линии напряженности перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны. В качестве замкнутой поверхности мысленно построим цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна ей. Так как образующие цилиндра параллельны линиям напряженности (угол между векторами 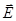 и
и  1 равен 900, cos900=0), то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равен сумме потоков сквозь его основания (площади оснований равны и для основания Еn совпадает с Е cos00=1
1 равен 900, cos900=0), то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равен сумме потоков сквозь его основания (площади оснований равны и для основания Еn совпадает с Е cos00=1 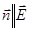 ), т. е. равен 2ЕS. Заряд, заключенный внутри построенной цилиндрической поверхности, равен
), т. е. равен 2ЕS. Заряд, заключенный внутри построенной цилиндрической поверхности, равен 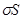 . Согласно теореме Гаусса,
. Согласно теореме Гаусса, 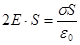 , откуда
, откуда
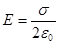 (1.21)
(1.21)
Из формулы вытекает, что Е не зависит от длины цилиндра, т. е. напряженность поля на любых расстояниях одинакова по модулю, иными словами, поле равномерно заряженной плоскости равномерно.
Ответ: поле равномерно заряженной бесконечной плоскости равно 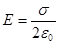 .
.
Задача 7. Покажите и рассчитайте поле двух бесконечных параллельных разноименно заряженных плоскостей.
Поле двух бесконечных параллельных разноименно заряженных плоскостей. Пусть плоскости заряжены равномерно разноименными зарядами с поверхностными плотностями 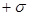 и
и 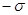 . Поле таких плоскостей найдем как суперпозицию плоскостей, создаваемых каждой из плоскостей в отдельности.
. Поле таких плоскостей найдем как суперпозицию плоскостей, создаваемых каждой из плоскостей в отдельности.

На рисунке 1.18 сплошные стрелки соответствуют полю от положительно заряженной плоскости, пунктирные – от отрицательной плоскости. Слева и справа от плоскостей областей I и III поля вычитаются (линии напряженности направлены навстречу друг другу), поэтому здесь напряженность поля Е=0. В области II между плоскостями Е=Е++Е-, поэтому результирующая напряженность
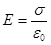 (1.22)
(1.22)

Рис. 1.18
Ответ: поле двух бесконечных параллельных разноименно заряженных плоскостей равно 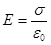 .
.